Zákon rozdelenia diskrétnej náhodnej premennej. Príklady riešenia problémov

Náhodná premenná nazýva sa premenná, ktorá ako výsledok každého testu nadobúda jednu predtým neznámu hodnotu v závislosti od náhodných príčin. Náhodné premenné sa označujú veľkými písmenami s latinskými písmenami: $X,\ Y,\ Z,\ \bodky $ Náhodné premenné môžu byť diskrétne a nepretržitý.

Diskrétna náhodná premenná- je to taká náhodná premenná, ktorej hodnoty môžu byť len spočítateľné, to znamená buď konečné alebo spočítateľné. Počitateľnosť znamená, že hodnoty náhodná premenná môžu byť očíslované.

Príklad 1 . Uveďme príklady diskrétnych náhodných premenných:

a) počet zásahov do terča $n$ výstrelmi, tu sú možné hodnoty $0,\ 1,\ \bodky,\ n$.

b) počet erbov, ktoré vypadli pri hode mincou, tu sú možné hodnoty $0,\ 1,\ \bodky,\ n$.

c) počet lodí, ktoré dorazili na palubu (počítateľný súbor hodnôt).

d) počet hovorov prichádzajúcich do ústredne (počítateľný súbor hodnôt).

1. Zákon rozdelenia pravdepodobnosti diskrétnej náhodnej premennej.

Diskrétna náhodná premenná $X$ môže nadobúdať hodnoty $x_1,\bodky,\ x_n$ s pravdepodobnosťou $p\left(x_1\right),\\dots ,\p\left(x_n\right)$. Korešpondencia medzi týmito hodnotami a ich pravdepodobnosťami sa nazýva distribučný zákon diskrétnej náhodnej premennej. Spravidla sa táto korešpondencia špecifikuje pomocou tabuľky, v ktorej prvom riadku sú uvedené hodnoty $x_1,\bodky,\ x_n$ a v druhom riadku sú pravdepodobnosti zodpovedajúce týmto hodnotám $ p_1,\bodky,\ p_n$.

$\begin(pole)(|c|c|)
\hline
X_i & x_1 & x_2 & \dots & x_n \\
\hline
p_i & p_1 & p_2 & \dots & p_n \\
\hline
\end(pole)$

Príklad 2 . Nech náhodná premenná $X$ je počet bodov hodených pri hode kockou. Takáto náhodná premenná $X$ môže nadobúdať nasledujúce hodnoty $1,\ 2,\ 3,\ 4,\ 5,\ 6$. Pravdepodobnosti všetkých týchto hodnôt sa rovnajú $ 1/6 $. Potom zákon rozdelenia pravdepodobnosti pre náhodnú premennú $X$:

$\begin(pole)(|c|c|)
\hline
1 & 2 & 3 & 4 & 5 & 6 \\
\hline

\hline
\end(pole)$

Komentujte. Keďže udalosti $1,\ 2,\ \bodky ,\ 6$ tvoria ucelenú skupinu udalostí v zákone rozdelenia diskrétnej náhodnej premennej $X$, súčet pravdepodobností sa musí rovnať jednej, t.j. $\sum( p_i) = 1 $.

2. Matematické očakávanie diskrétnej náhodnej premennej.

Matematické očakávanie náhodnej premennej určuje jeho "centrálnu" hodnotu. Pre diskrétnu náhodnú premennú sa matematické očakávanie vypočíta ako súčet súčinov hodnôt $x_1,\bodky,\x_n$ a pravdepodobností $p_1,\bodky,\p_n$ zodpovedajúcich týmto hodnotám, t.j.: $M\vľavo(X\vpravo)=\súčet ^n_(i=1)(p_ix_i)$. V anglickej literatúre sa používa iný zápis $E\left(X\right)$.

Vlastnosti očakávania$M\vľavo(X\vpravo)$:

1. $M\left(X\right)$ je medzi najmenším a najvyššie hodnoty náhodná premenná $X$.
2. Matematické očakávanie konštanty sa rovná samotnej konštante, t.j. $M\vľavo(C\vpravo)=C$.
3. Konštantný faktor možno vyňať zo znamienka očakávania: $M\left(CX\right)=CM\left(X\right)$.
4. Matematické očakávanie súčtu náhodných premenných sa rovná súčtu ich matematických očakávaní: $M\left(X+Y\right)=M\left(X\right)+M\left(Y\right)$.
5. Matematické očakávanie súčinu nezávislých náhodných premenných sa rovná súčinu ich matematických očakávaní: $M\vľavo(XY\vpravo)=M\vľavo(X\vpravo)M\vľavo(Y\vpravo)$.

Príklad 3 . Nájdime matematické očakávanie náhodnej premennej $X$ z príkladu $2$.

$$M\left(X\right)=\sum^n_(i=1)(p_ix_i)=1\cdot ((1)\over (6))+2\cdot ((1)\over (6) )+3\cdot ((1)\nad (6))+4\cdot ((1)\nad (6))+5\cdot ((1)\nad (6))+6\cdot ((1) )\nad (6))=3,5.$$

Môžeme si všimnúť, že $M\left(X\right)$ je medzi najmenšou ($1$) a najväčšou ($6$) hodnotou náhodnej premennej $X$.

Príklad 4 . Je známe, že matematické očakávanie náhodnej premennej $X$ sa rovná $M\left(X\right)=2$. Nájdite matematické očakávanie náhodnej premennej $3X+5$.

Použitím vyššie uvedených vlastností dostaneme $M\vľavo(3X+5\vpravo)=M\vľavo(3X\vpravo)+M\vľavo(5\vpravo)=3M\vľavo(X\vpravo)+5=3\ cdot 2 +5 = 11 $.

Príklad 5 . Je známe, že matematické očakávanie náhodnej premennej $X$ sa rovná $M\left(X\right)=4$. Nájdite matematické očakávanie náhodnej premennej $2X-9$.

Pomocou vyššie uvedených vlastností dostaneme $M\vľavo(2X-9\vpravo)=M\vľavo(2X\vpravo)-M\vľavo(9\vpravo)=2M\vľavo(X\vpravo)-9=2\ cdot 4 -9=-1$.

3. Disperzia diskrétnej náhodnej premennej.

Možné hodnoty náhodné premenné s rovnakými matematickými očakávaniami sa môžu okolo svojich priemerov rozptýliť rôznymi spôsobmi. Napríklad v dvoch skupinách študentov bolo priemerné skóre na skúške z teórie pravdepodobnosti 4, ale v jednej skupine boli všetci dobrí študenti av druhej skupine iba študenti C a vynikajúci študenti. Preto existuje potreba takých číselná charakteristika náhodná premenná, ktorá by ukazovala rozptyl hodnôt náhodnej premennej okolo jej matematického očakávania. Táto vlastnosť je disperzia.

Disperzia diskrétnej náhodnej premennej$X$ je:

$$D\vľavo(X\vpravo)=\súčet^n_(i=1)(p_i(\vľavo(x_i-M\vľavo(X\vpravo)\vpravo))^2).\ $$

V anglickej literatúre sa používa zápis $V\left(X\right),\ Var\left(X\right)$. Veľmi často sa rozptyl $D\left(X\right)$ počíta podľa vzorca $D\left(X\right)=\sum^n_(i=1)(p_ix^2_i)-(\left(M\ vľavo(X \vpravo)\vpravo))^2$.

Vlastnosti disperzie$D\vľavo(X\vpravo)$:

1. Disperzia je vždy väčšia alebo rovná nule, t.j. $D\vľavo(X\vpravo)\ge 0$.
2. Disperzia z konštanty sa rovná nule, t.j. $D\vľavo(C\vpravo)=0$.
3. Konštantný faktor je možné odobrať zo znamienka rozptylu za predpokladu, že je na druhú, t.j. $D\left(CX\right)=C^2D\left(X\right)$.
4. Rozptyl súčtu nezávislých náhodných veličín sa rovná súčtu ich rozptylov, t.j. $D\vľavo(X+Y\vpravo)=D\vľavo(X\vpravo)+D\vľavo(Y\vpravo)$.
5. Rozptyl rozdielu nezávislých náhodných veličín sa rovná súčtu ich rozptylov, t.j. $D\vľavo(X-Y\vpravo)=D\vľavo(X\vpravo)+D\vľavo(Y\vpravo)$.

Príklad 6 . Vypočítajme rozptyl náhodnej premennej $X$ z príkladu $2$.

$$D\vľavo(X\vpravo)=\súčet^n_(i=1)(p_i(\vľavo(x_i-M\vľavo(X\vpravo)\vpravo))^2)=((1)\nad (6))\cdot (\left(1-3,5\right))^2+((1)\over (6))\cdot (\left(2-3,5\right))^2+ \bodky +((1)\viac ako (6))\cdot (\left(6-3,5\right))^2=((35)\nad (12))\približne 2,92,$$

Príklad 7 . Je známe, že rozptyl náhodnej premennej $X$ sa rovná $D\left(X\right)=2$. Nájdite rozptyl náhodnej premennej $4X+1$.

Pomocou vyššie uvedených vlastností nájdeme $D\left(4X+1\right)=D\left(4X\right)+D\left(1\right)=4^2D\left(X\right)+0= 16D\ vľavo(X\vpravo)=16\cdot 2=32$.

Príklad 8 . Je známe, že rozptyl $X$ sa rovná $D\left(X\right)=3$. Nájdite rozptyl náhodnej premennej $3-2X$.

Pomocou vyššie uvedených vlastností nájdeme $D\left(3-2X\right)=D\left(3\right)+D\left(2X\right)=0+2^2D\left(X\right)= 4D\ vľavo(X\vpravo)=4\cdot 3=12$.

4. Distribučná funkcia diskrétnej náhodnej premennej.

Spôsob reprezentácie diskrétnej náhodnej premennej vo forme distribučného radu nie je jediný, a čo je najdôležitejšie, nie je univerzálny, pretože spojitú náhodnú premennú nie je možné špecifikovať pomocou distribučného radu. Existuje ďalší spôsob, ako reprezentovať náhodnú premennú - distribučnú funkciu.

distribučná funkcia náhodná premenná $X$ je funkcia $F\left(x\right)$, ktorá určuje pravdepodobnosť, že náhodná premenná $X$ nadobudne hodnotu menšiu ako nejaká pevná hodnota $x$, t.j. $F\left(x\) vpravo)$ )=P\vľavo(X< x\right)$

Vlastnosti distribučnej funkcie:

1. $0\le F\left(x\right)\le 1$.
2. Pravdepodobnosť, že náhodná premenná $X$ nadobudne hodnoty z intervalu $\left(\alpha ;\ \beta \right)$, sa rovná rozdielu medzi hodnotami distribučnej funkcie na koncoch tohto intervalu : $P\left(\alpha< X < \beta \right)=F\left(\beta \right)-F\left(\alpha \right)$
3. $F\left(x\right)$ - neklesá.
4. $(\mathop(lim)_(x\to -\infty ) F\left(x\right)=0\ ),\ (\mathop(lim)_(x\to +\infty ) F\left(x \vpravo)=1\ )$.

Príklad 9 . Nájdite distribučnú funkciu $F\left(x\right)$ pre distribučný zákon diskrétnej náhodnej premennej $X$ z príkladu $2$.

$\begin(pole)(|c|c|)
\hline
1 & 2 & 3 & 4 & 5 & 6 \\
\hline
1/6 & 1/6 & 1/6 & 1/6 & 1/6 & 1/6 \\
\hline
\end(pole)$

Ak $x\le 1$, potom samozrejme $F\left(x\right)=0$ (vrátane $x=1$ $F\left(1\right)=P\left(X< 1\right)=0$).

Ak 1 dolár< x\le 2$, то $F\left(x\right)=P\left(X=1\right)=1/6$.

Ak 2 doláre< x\le 3$, то $F\left(x\right)=P\left(X=1\right)+P\left(X=2\right)=1/6+1/6=1/3$.

Ak 3 doláre< x\le 4$, то $F\left(x\right)=P\left(X=1\right)+P\left(X=2\right)+P\left(X=3\right)=1/6+1/6+1/6=1/2$.

Ak 4 doláre< x\le 5$, то $F\left(X\right)=P\left(X=1\right)+P\left(X=2\right)+P\left(X=3\right)+P\left(X=4\right)=1/6+1/6+1/6+1/6=2/3$.

Ak 5 dolárov< x\le 6$, то $F\left(x\right)=P\left(X=1\right)+P\left(X=2\right)+P\left(X=3\right)+P\left(X=4\right)+P\left(X=5\right)=1/6+1/6+1/6+1/6+1/6=5/6$.

Ak $x > 6$, potom $F\vľavo(x\vpravo)=P\vľavo(X=1\vpravo)+P\vľavo(X=2\vpravo)+P\vľavo(X=3\vpravo) + P\vľavo(X=4\vpravo)+P\vľavo(X=5\vpravo)+P\vľavo(X=6\vpravo)=1/6+1/6+1/6+1/6+ 1 /6+1/6=1$.

Takže $F(x)=\vľavo\(\začiatok(matica)
0,\ na\ x\le 1,\\
1/6, o \ 1< x\le 2,\\
1/3,\ na\ 2< x\le 3,\\
1/2, o \ 3< x\le 4,\\
2/3,\ o\ 4< x\le 5,\\
6.5., \ o \ 4< x\le 5,\\
1,\ pre \ x > 6.
\end(matica)\right.$

Definícia 2.3. Náhodná premenná označená X sa nazýva diskrétna, ak naberá konečný alebo spočítateľný súbor hodnôt, t.j. množina je konečná alebo spočítateľná množina.

Zvážte príklady diskrétnych náhodných premenných.

1. Raz sa hádžu dve mince. Počet erbov v tomto experimente je náhodná veličina X. Jeho možné hodnoty sú 0,1,2, t.j. je konečná množina.

2. Zaznamenáva sa počet volaní sanitky počas daného časového obdobia. Náhodná hodnota X– počet hovorov. Jeho možné hodnoty sú 0, 1, 2, 3, ..., t.j. =(0,1,2,3,...) je spočítateľná množina.

3. V skupine je 25 žiakov. V niektorý deň sa zaznamenáva počet žiakov, ktorí prišli na vyučovanie – náhodná veličina X. Jeho možné hodnoty sú: 0, 1, 2, 3, ..., 25 t.j. =(0, 1, 2, 3, ..., 25).

Všetkých 25 ľudí v príklade 3 síce nemôže vynechať hodiny, ale náhodnú premennú X môže nadobudnúť túto hodnotu. To znamená, že hodnoty náhodnej premennej majú rôzne pravdepodobnosti.

Zvážte matematický model diskrétnej náhodnej premennej.

Nech sa drží náhodný experiment, ktorý zodpovedá konečnému alebo spočítateľnému priestoru elementárnych udalostí . Uvažujme priradenie tohto priestoru na množinu reálnych čísel, t.j. každú elementárnu udalosť priradíme k nejakému reálnemu číslu , . Množina čísel v tomto prípade môže byť konečná alebo spočítateľná, t.j. alebo

Systém podmnožín, ktorý zahŕňa akúkoľvek podmnožinu vrátane jednobodovej, tvorí -algebru číselnej množiny (-konečne alebo spočítateľne).

Pretože každá elementárna udalosť je spojená s určitými pravdepodobnosťami p i(v prípade konečných všetkých ), a , potom môžeme každej hodnote náhodnej premennej priradiť určitú pravdepodobnosť p i, také že .

Nechaj X je ľubovoľné reálne číslo. Označiť R X (x) pravdepodobnosť, že náhodná premenná X nadobudol hodnotu rovnajúcu sa X, t.j. P X (x) \u003d P (X \u003d x). Potom funkcia R X (x) môže vziať kladné hodnoty len pre tie hodnoty X, ktoré patria do konečnej alebo spočítateľnej množiny a pre všetky ostatné hodnoty pravdepodobnosť tejto hodnoty P X (x) = 0.

Definovali sme teda množinu hodnôt -algebra ako systém akýchkoľvek podmnožín a pre každú udalosť ( X=x) porovnala pravdepodobnosť pre akékoľvek , t.j. vytvoril priestor pravdepodobnosti.

Napríklad priestor elementárnych udalostí experimentu spočívajúceho v hádzaní symetrickej mince dvakrát pozostáva zo štyroch elementárnych udalostí: , kde

Keď sa dvakrát hodila minca, vypadli dve mriežky; keď sa dvakrát hodila minca, vypadli dva erby;

Pri prvom hode mincou vypadol rošt a pri druhom erb;

Pri prvom hode mincou vypadol erb a pri druhom rošt.

Nech náhodná premenná X je počet výpadkov mriežky. Je definovaný na a súbore jeho hodnôt . Všetky možné podmnožiny vrátane jednobodových tvoria - algebru, t.j. =(Ø, (1), (2), (0,1), (0,2), (1,2), (0,1,2)).

Pravdepodobnosť udalosti ( X = x i}, і = 1,2,3 , definujeme ako pravdepodobnosť výskytu udalosti, ktorá je jej prototypom:

Teda pri základných udalostiach ( X = x i) nastaviť číselnú funkciu R X, takže .

Definícia 2.4. Distribučný zákon diskrétnej náhodnej premennej je množina párov čísel (x i, p i), kde x i sú možné hodnoty náhodnej premennej a p i sú pravdepodobnosti, s ktorými tieto hodnoty nadobúda, a .

Najjednoduchšia forma nastavenie distribučného zákona diskrétnej náhodnej premennej je tabuľka, ktorá uvádza možné hodnoty náhodnej premennej a zodpovedajúce pravdepodobnosti:

			…		…
			…		…

Takáto tabuľka sa nazýva distribučný riadok. Aby bola distribučná séria viac vizuálna, je znázornená graficky: na osi Oh dať bodky x i a kresliť z nich kolmice dĺžky p i. Výsledné body sa spoja a získa sa mnohouholník, ktorý je jednou z foriem distribučného zákona (obr. 2.1).

Ak teda chcete nastaviť diskrétnu náhodnú premennú, musíte nastaviť jej hodnoty a zodpovedajúce pravdepodobnosti.

Príklad 2.2. Akceptor peňazí automatu sa spustí vždy, keď s pravdepodobnosťou padne minca R. Akonáhle to funguje, mince sa neznižujú. Nechaj X- počet mincí, ktoré sa musia znížiť pred spustením zariadenia na príjem peňazí. Zostrojte sériu rozdelenia diskrétnej náhodnej premennej X.

Riešenie. Možné hodnoty náhodnej premennej X: x 1 \u003d 1, x 2 \u003d 2, ..., x k \u003d k, ... Poďme nájsť pravdepodobnosti týchto hodnôt: p 1 je pravdepodobnosť, že zásuvka na peniaze bude fungovať pri prvom zostupe, a p1 = p; p 2 - pravdepodobnosť, že sa uskutočnia dva pokusy. K tomu je potrebné, aby: 1) pri prvom pokuse nefungoval príjemca peňazí; 2) na druhý pokus - podarilo sa. Pravdepodobnosť tejto udalosti je (1–r)r. Podobne a tak ďalej, . Rozsah distribúcie X bude mať formu

	1	2	3	…	do	…
	R	qp	q 2 p		q r -1 str

Všimnite si, že pravdepodobnosti r do tvoria geometrickú postupnosť s menovateľom: 1 – p = q, q<1, takže toto rozdelenie pravdepodobnosti sa nazýva geometrický.

Predpokladajme ďalej, že bol skonštruovaný matematický model experiment opísaný diskrétnou náhodnou premennou X a zvážte výpočet pravdepodobnosti výskytu svojvoľných udalostí.

Nech ľubovoľná udalosť obsahuje konečnú alebo spočítateľnú množinu hodnôt x i: A= {x 1 , x 2 ,..., x i , ...) .Udalosť ALE možno reprezentovať ako spojenie nezlučiteľných udalostí v tvare : . Potom aplikovaním Kolmogorovovej axiómy 3 , dostaneme

keďže sme určili, že pravdepodobnosti výskytu udalostí sa rovnajú pravdepodobnostiam výskytu udalostí, ktoré sú ich prototypmi. To znamená, že pravdepodobnosť akejkoľvek udalosti , , možno vypočítať podľa vzorca , keďže táto udalosť môže byť reprezentovaná ako spojenie udalostí, kde .

Potom distribučná funkcia F(х) = Р(–<Х<х) sa nachádza podľa vzorca. Z toho vyplýva, že distribučná funkcia diskrétnej náhodnej premennej X je nespojitá a skokovo sa zväčšuje, t. j. ide o krokovú funkciu (obr. 2.2):

Ak je množina konečná, potom je počet členov vo vzorci konečný, ak je spočítateľný, potom je spočítateľný aj počet členov.

Príklad 2.3. Technické zariadenie pozostáva z dvoch prvkov, ktoré pracujú nezávisle na sebe. Pravdepodobnosť zlyhania prvého prvku v čase T je 0,2 a pravdepodobnosť zlyhania druhého prvku je 0,1. Náhodná hodnota X- počet neúspešných prvkov v čase T. Nájdite distribučnú funkciu náhodnej premennej a zostavte jej graf.

Riešenie. Priestor elementárnych dejov experimentu, ktorý spočíva v štúdiu spoľahlivosti dvoch prvkov technického zariadenia, je určený štyrmi elementárnymi dejmi , , , : – oba prvky sú v poriadku; - prvý prvok je prevádzkyschopný, druhý je chybný; - prvý prvok je chybný, druhý je prevádzkyschopný; – oba prvky sú chybné. Každá z elementárnych udalostí môže byť vyjadrená pomocou elementárnych udalostí priestorov a , kde – prvý prvok je použiteľný; - prvý prvok je mimo prevádzky; – druhý prvok je použiteľný; - Druhý prvok je mimo prevádzky. Potom , a keďže prvky technického zariadenia fungujú nezávisle od seba, potom

8. Aká je pravdepodobnosť, že hodnoty diskrétnej náhodnej premennej patria do intervalu?

Môžeme vyzdvihnúť najbežnejšie zákony distribúcie diskrétnych náhodných premenných:

• Zákon binomického rozdelenia
• Poissonov zákon o rozdelení
• Zákon geometrického rozdelenia
• Hypergeometrický distribučný zákon

Pre dané rozdelenia diskrétnych náhodných veličín sa podľa určitých „vzorcov“ uskutočňuje výpočet pravdepodobnosti ich hodnôt, ako aj číselných charakteristík (matematické očakávanie, rozptyl a pod.). Preto je veľmi dôležité poznať tieto typy rozvodov a ich základné vlastnosti.

1. Zákon binomického rozdelenia.

Diskrétna náhodná premenná $X$ podlieha binomickému rozdeleniu pravdepodobnosti, ak nadobúda hodnoty $0,\ 1,\ 2,\ \bodky,\ n$ s pravdepodobnosťami $P\left(X=k\right)= C^k_n\cdot p^k\cdot (\left(1-p\right))^(n-k)$. V skutočnosti je náhodná premenná $X$ počet výskytov udalosti $A$ v $n$ nezávislých pokusoch. Zákon rozdelenia pravdepodobnosti pre náhodnú premennú $X$:

$\begin(pole)(|c|c|)
\hline
X_i & 0 & 1 & \dots & n \\
\hline
p_i & P_n\left(0\right) & P_n\left(1\right) & \dots & P_n\left(n\right) \\
\hline
\end(pole)$

Pre takúto náhodnú premennú je očakávanie $M\left(X\right)=np$, rozptyl je $D\left(X\right)=np\left(1-p\right)$.

Príklad . V rodine sú dve deti. Za predpokladu, že pravdepodobnosť narodenia chlapca a dievčaťa je 0,5 $, nájdite zákon rozdelenia náhodnej premennej $\xi $ - počet chlapcov v rodine.

Nech náhodná premenná $\xi $ je počet chlapcov v rodine. Hodnoty, ktoré $\xi:\ 0,\ ​​​​1,\ 2$ môže nadobudnúť. Pravdepodobnosť týchto hodnôt možno nájsť pomocou vzorca $P\left(\xi =k\right)=C^k_n\cdot p^k\cdot (\left(1-p\right))^(n-k )$, kde $n =2$ - počet nezávislých pokusov, $p=0,5$ - pravdepodobnosť výskytu udalosti v sérii $n$ pokusov. Dostaneme:

$P\left(\xi =0\right)=C^0_2\cdot (0,5)^0\cdot (\left(1-0,5\right))^(2-0)=(0, 5)^2 = 0,25; $

$P\left(\xi =1\right)=C^1_2\cdot 0,5\cdot (\left(1-0,5\right))^(2-1)=2\cdot 0,5\ cdot 0,5=0,5;$

$P\left(\xi =2\right)=C^2_2\cdot (0,5)^2\cdot (\left(1-0,5\right))^(2-2)=(0, 5)^2=0,25.$

Potom distribučný zákon náhodnej premennej $\xi $ je korešpondencia medzi hodnotami $0,\ 1,\ 2$ a ich pravdepodobnosťami, t.j.:

$\begin(pole)(|c|c|)
\hline
\xi & 0 & 1 & 2 \\
\hline
P(\xi) & 0,25 & 0,5 & 0,25 \\
\hline
\end(pole)$

Súčet pravdepodobností v distribučnom zákone sa musí rovnať $1$, t.j. $\sum _(i=1)^(n)P(\xi _((\rm i)))=0,25+0,5+0, 25 = 1 USD.

Očakávanie $M\left(\xi \right)=np=2\cdot 0,5=1$, rozptyl $D\left(\xi \right)=np\left(1-p\right)=2\ cdot 0,5\ cdot 0,5=0,5$, štandardná odchýlka $\sigma \left(\xi \right)=\sqrt(D\left(\xi \right))=\sqrt(0,5)\približne 0,707 $.

2. Poissonov zákon rozdelenia.

Ak diskrétna náhodná premenná $X$ môže nadobúdať iba nezáporné celočíselné hodnoty $0,\ 1,\ 2,\ \bodky,\ n$ s pravdepodobnosťou $P\left(X=k\right)=((( \lambda )^k )\over (k}\cdot e^{-\lambda }$, то говорят, что она подчинена закону распределения Пуассона с параметром $\lambda $. Для такой случайной величины математическое ожидание и дисперсия равны между собой и равны параметру $\lambda $, то есть $M\left(X\right)=D\left(X\right)=\lambda $.!}

Komentujte. Zvláštnosťou tohto rozdelenia je, že na základe experimentálnych údajov nájdeme odhady $M\left(X\right),\D\left(X\right)$, ak sú získané odhady blízko seba, potom majú dôvod tvrdiť, že náhodná premenná podlieha Poissonovmu zákonu rozdelenia.

Príklad . Príkladmi náhodných premenných podliehajúcich Poissonovmu zákonu o distribúcii môžu byť: počet áut, ktoré budú zajtra obsluhované čerpacou stanicou; počet chybných položiek vo vyrobenom produkte.

Príklad . Závod poslal na základňu produkty v hodnote 500 $. Pravdepodobnosť poškodenia produktu počas prepravy je 0,002 USD. Nájdite distribučný zákon náhodnej premennej $X$, ktorý sa rovná počtu poškodených produktov; čo sa rovná $M\left(X\right),\D\left(X\right)$.

Nech je diskrétna náhodná premenná $X$ počet poškodených položiek. Takáto náhodná premenná podlieha Poissonovmu zákonu rozdelenia s parametrom $\lambda =np=500\cdot 0,002=1$. Pravdepodobnosť hodnôt je $P\left(X=k\right)=(((\lambda )^k)\over (k)}\cdot e^{-\lambda }$. Очевидно, что все вероятности всех значений $X=0,\ 1,\ \dots ,\ 500$ перечислить невозможно, поэтому мы ограничимся лишь первыми несколькими значениями.!}

$P\left(X=0\right)=((1^0)\over (0}\cdot e^{-1}=0,368;$!}

$P\left(X=1\right)=((1^1)\over (1}\cdot e^{-1}=0,368;$!}

$P\left(X=2\right)=((1^2)\over (2}\cdot e^{-1}=0,184;$!}

$P\left(X=3\right)=((1^3)\over (3}\cdot e^{-1}=0,061;$!}

$P\left(X=4\right)=((1^4)\over (4}\cdot e^{-1}=0,015;$!}

$P\left(X=5\right)=((1^5)\over (5}\cdot e^{-1}=0,003;$!}

$P\left(X=6\right)=((1^6)\over (6}\cdot e^{-1}=0,001;$!}

$P\left(X=k\right)=(((\lambda )^k)\over (k}\cdot e^{-\lambda }$!}

Distribučný zákon náhodnej premennej $X$:

$\begin(pole)(|c|c|)
\hline
X_i & 0 & 1 & 2 & 3 & 4 & 5 & 6 & ... & k \\
\hline
P_i & 0,368; & 0,368 & 0,184 & 0,061 & 0,015 & 0,003 & 0,001 & ... & (((\lambda )^k)\over (k}\cdot e^{-\lambda } \\!}
\hline
\end(pole)$

Pre takúto náhodnú premennú sú matematické očakávania a rozptyl rovnaké a rovné parametru $\lambda $, t.j. $M\left(X\right)=D\left(X\right)=\lambda =1 $.

3. Geometrický zákon rozloženia.

Ak diskrétna náhodná premenná $X$ môže nadobúdať iba prirodzené hodnoty $1,\ 2,\ \bodky,\ n$ s pravdepodobnosťou $P\left(X=k\right)=p(\left(1-p\) vpravo)) ^(k-1),\ k=1,\ 2,\ 3,\ \bodky $, potom hovoríme, že takáto náhodná premenná $X$ podlieha geometrickému zákonu rozdelenia pravdepodobnosti. V skutočnosti sa zdá, že geometrické rozdelenie je Bernoulliho pokusom o prvý úspech.

Príklad . Príklady náhodných premenných, ktoré majú geometrické rozdelenie, môžu byť: počet výstrelov pred prvým zásahom do cieľa; počet testov zariadenia pred prvou poruchou; počet hodov mincou pred prvým heads up atď.

Matematické očakávanie a rozptyl náhodnej premennej podliehajúcej geometrickému rozdeleniu sú $M\left(X\right)=1/p$, $D\left(X\right)=\left(1-p\right) /p^ 2 $.

Príklad . Na ceste pohybu rýb k miestu trenia je 4$ zámok. Pravdepodobnosť, že ryba prejde každou plavebnou komorou je $p=3/5$. Zostrojte distribučný rad náhodnej premennej $X$ - počet plavebných komôr, ktoré ryba prešla pred prvým zastavením v plavebnej komore. Nájdite $M\left(X\right),\D\left(X\right),\\sigma \left(X\right)$.

Nech je náhodná premenná $X$ počet stavidiel, ktoré ryba prešla pred prvou zastávkou pri stavidle. Takáto náhodná veličina podlieha geometrickému zákonu rozdelenia pravdepodobnosti. Hodnoty, ktoré môže nadobudnúť náhodná premenná $X, sú: 1, 2, 3, 4. Pravdepodobnosť týchto hodnôt sa vypočíta podľa vzorca: $P\left(X=k\right)=pq^( k-1)$, kde: $ p=2/5$ - pravdepodobnosť chytenia rýb cez plavebnú komoru, $q=1-p=3/5$ - pravdepodobnosť, že ryba prejde plavebnou komorou, $k=1, \ 2,\ 3,\ 4 $.

$P\left(X=1\right)=((2)\over (5))\cdot (\left(((3)\over (5))\right))^0=((2)\ nad(5))=0,4;$

$P\left(X=2\right)=((2)\over (5))\cdot ((3)\over (5))=((6)\over (25))=0,24; $

$P\left(X=3\right)=((2)\over (5))\cdot (\left(((3)\over (5))\right))^2=((2)\ nad (5))\cdot ((9)\nad (25))=((18)\viac ako (125))=0,144;$

$P\left(X=4\right)=((2)\over (5))\cdot (\left(((3)\over (5))\right))^3+(\left(( (3)\nad (5))\vpravo))^4=((27)\viac ako (125))=0,216,$

$\begin(pole)(|c|c|)
\hline
X_i & 1 & 2 & 3 & 4 \\
\hline
P\left(X_i\right) & 0,4 & 0,24 & 0,144 & 0,216 \\
\hline
\end(pole)$

Očakávaná hodnota:

$M\left(X\right)=\sum^n_(i=1)(x_ip_i)=1\cdot 0,4+2\cdot 0,24+3\cdot 0,144+4\cdot 0,216=2,176,$

Rozptyl:

$D\left(X\right)=\sum^n_(i=1)(p_i(\left(x_i-M\left(X\right)\right))^2=)0,4\cdot (\ left(1-2,176\right))^2+0,24\cdot (\left(2-2,176\right))^2+0,144\cdot (\left(3-2,176\right))^2+$

$+\ 0,216\cdot (\left(4-2,176\right))^2\približne 1,377,$

štandardná odchýlka:

$\sigma \left(X\right)=\sqrt(D\left(X\right))=\sqrt(1 377)\približne 1 173,$

4. Zákon hypergeometrického rozdelenia.

Ak existuje $N$ objektov, medzi ktorými má danú vlastnosť $m$ objektov. Náhodne sa bez náhrady extrahuje $n$ objektov, medzi ktorými je $k$ objektov, ktoré majú danú vlastnosť. Hypergeometrické rozdelenie umožňuje odhadnúť pravdepodobnosť, že presne $k$ objektov vo vzorke má danú vlastnosť. Nech náhodná premenná $X$ je počet objektov vo vzorke, ktoré majú danú vlastnosť. Potom pravdepodobnosti hodnôt náhodnej premennej $ X $:

$P\left(X=k\right)=((C^k_mC^(n-k)_(N-m))\over (C^n_N))$

Komentujte. Štatistická funkcia HYPERGEOMET Sprievodcu funkciou Excel $f_x$ vám umožňuje určiť pravdepodobnosť, že určitý počet pokusov bude úspešný.

$f_x\to $ štatistické$\až $ HYPERGEOMET$\až $ OK. Zobrazí sa dialógové okno, ktoré musíte vyplniť. V grafe Počet_úspechov_v_vzorke uveďte hodnotu $k$. veľkosť vzorky sa rovná $n$. V grafe Počet_úspechov_v_populácii uveďte hodnotu $ m $. Veľkosť_populácie rovná sa $N$.

Matematické očakávanie a rozptyl diskrétnej náhodnej premennej $X$ podliehajúcej zákonu o geometrickom rozdelení sú $M\left(X\right)=nm/N$, $D\left(X\right)=((nm\left) (1 -((m)\cez (N))\vpravo)\vľavo(1-((n)\cez (N))\vpravo))\cez (N-1))$.

Príklad . Úverové oddelenie banky zamestnáva 5 špecialistov s vyšším finančným vzdelaním a 3 špecialistov s vyšším právnickým vzdelaním. Vedenie banky sa rozhodlo vyslať 3 špecialistov na pokročilé školenie, pričom ich vybralo náhodne.

a) Vytvoriť distribučný rad počtu špecialistov s vyšším finančným vzdelaním, ktorí môžu byť nasmerovaní na pokročilú odbornú prípravu;

b) Nájdite číselné charakteristiky tohto rozdelenia.

Nech je náhodná premenná $X$ počet špecialistov s vyšším finančným vzdelaním spomedzi troch vybraných. Hodnoty, ktoré môže nadobudnúť $X:0,\ 1,\ 2,\ 3 $. Táto náhodná premenná $X$ je rozdelená podľa hypergeometrického rozdelenia s nasledujúcimi parametrami: $N=8$ - veľkosť populácie, $m=5$ - počet úspechov v populácii, $n=3$ - veľkosť vzorky, $ k=0,\ 1, \ 2,\ 3$ - počet úspechov vo vzorke. Potom možno pravdepodobnosti $P\left(X=k\right)$ vypočítať pomocou vzorca: $P(X=k)=(C_(m)^(k) \cdot C_(N-m)^(n-k) \ nad C_( N)^(n) ) $. Máme:

$P\left(X=0\right)=((C^0_5\cdot C^3_3)\over (C^3_8))=((1)\over (56))\približne 0,018;$

$P\left(X=1\right)=((C^1_5\cdot C^2_3)\over (C^3_8))=((15)\over (56))\približne 0,268;$

$P\left(X=2\right)=((C^2_5\cdot C^1_3)\over (C^3_8))=((15)\over (28))\približne 0,536;$

$P\left(X=3\right)=((C^3_5\cdot C^0_3)\over (C^3_8))=((5)\over (28))\približne 0,179,$

Potom distribučný rad náhodnej premennej $X$:

$\begin(pole)(|c|c|)
\hline
X_i & 0 & 1 & 2 & 3 \\
\hline
p_i & 0,018 & 0,268 & 0,536 & 0,179 \\
\hline
\end(pole)$

Vypočítajme číselné charakteristiky náhodnej premennej $X$ pomocou všeobecných vzorcov hypergeometrického rozdelenia.

$M\vľavo(X\vpravo)=((nm)\nad (N))=((3\cdot 5)\nad (8))=((15)\nad (8))=1 875,$

$D\vľavo(X\vpravo)=((nm\vľavo(1-((m)\nad (N))\vpravo)\vľavo(1-((n)\nad (N))\vpravo)) \over (N-1))=((3\cdot 5\cdot \left(1-((5)\over (8))\right)\cdot \left(1-((3)\over (8) ))\vpravo))\nad (8-1))=((225)\nad (448))\približne 0,502,$

$\sigma \left(X\right)=\sqrt(D\left(X\right))=\sqrt(0,502)\približne 0,7085,$

Je daný distribučný rad diskrétnej náhodnej premennej. Nájdite chýbajúcu pravdepodobnosť a nakreslite distribučnú funkciu. Vypočítajte matematické očakávanie a rozptyl tejto hodnoty.

Náhodná premenná X má iba štyri hodnoty: -4, -3, 1 a 2. Každú z týchto hodnôt nadobúda s určitou pravdepodobnosťou. Keďže súčet všetkých pravdepodobností sa musí rovnať 1, chýbajúca pravdepodobnosť sa rovná:

0,3 + ? + 0,1 + 0,4 = 1,

Zostavte distribučnú funkciu náhodnej premennej X. Je známe, že distribučná funkcia , potom:

v dôsledku toho

Nakreslíme funkciu F(X) .

Matematické očakávanie diskrétnej náhodnej premennej sa rovná súčtu súčinov hodnoty náhodnej premennej a príslušnej pravdepodobnosti, t.j.

Rozptyl diskrétnej náhodnej premennej nájdeme podľa vzorca:

DODATOK

Prvky kombinatoriky Tu: - faktoriál čísla

Akcie na udalostiach Udalosť je akákoľvek skutočnosť, ktorá môže alebo nemusí nastať v dôsledku zážitku. Zlučovanie udalostí ALE a AT- táto udalosť OD, ktorá spočíva vo vzhľade alebo udalosti ALE alebo udalosti AT alebo obe udalosti súčasne. Označenie: ; Priesečník udalostí ALE a AT- táto udalosť OD, ktorá spočíva v súčasnom výskyte oboch udalostí. Označenie: ;

Klasická definícia pravdepodobnosti Pravdepodobnosť udalosti ALE je pomer počtu experimentov , priaznivé pre výskyt udalosti ALE k celkovému počtu experimentov :

Vzorec násobenia pravdepodobnosti Pravdepodobnosť udalosti možno nájsť pomocou vzorca: - pravdepodobnosť udalosti ALE, - pravdepodobnosť udalosti AT, - pravdepodobnosť udalosti AT za predpokladu, že udalosť ALE už sa stalo. Ak sú udalosti A a B nezávislé (výskyt jednej neovplyvňuje výskyt druhej), pravdepodobnosť udalosti je:

Vzorec sčítania pravdepodobnosti Pravdepodobnosť udalosti možno nájsť pomocou vzorca: Pravdepodobnosť udalosti ALE, Pravdepodobnosť udalosti AT, - pravdepodobnosť spoločného výskytu udalostí ALE a AT. Ak sú udalosti A a B nekompatibilné (nemôžu sa vyskytnúť súčasne), pravdepodobnosť udalosti je:

Vzorec úplnej pravdepodobnosti Nechajte udalosť ALE sa môže stať súčasne s jednou z udalostí , , …, Nazvime ich hypotézy. Tiež známy - pravdepodobnosť splnenia i-tá hypotéza a - pravdepodobnosť výskytu udalosti A počas vykonávania i hypotéza. Potom pravdepodobnosť udalosti ALE možno nájsť pomocou vzorca:

Bernoulliho schéma Nech sa vykoná n nezávislých testov. Pravdepodobnosť výskytu (úspešnosti) udalosti ALE v každom z nich je konštantná a rovnaká p, pravdepodobnosť zlyhania (t. j. nie výskyt udalosti ALE) q = 1 - p. Potom pravdepodobnosť výskytu kúspech v n testy možno nájsť podľa Bernoulliho vzorca: S najväčšou pravdepodobnosťou počet úspechov v Bernoulliho schéme je to počet výskytov nejakej udalosti, ktorý zodpovedá najvyššej pravdepodobnosti. Dá sa zistiť pomocou vzorca:

náhodné premenné diskrétne spojité (napr. počet dievčat v rodine s 5 deťmi) (napr. dostupnosť varnej kanvice) Numerické charakteristiky diskrétnych náhodných premenných Nech je diskrétna hodnota daná distribučným radom: X R , , …, - hodnoty náhodnej premennej X; , , …, sú zodpovedajúce pravdepodobnosti. distribučná funkcia Distribučná funkcia náhodnej premennej X sa nazýva funkcia uvedená na celej číselnej osi a rovná sa pravdepodobnosti, že X bude menej X:

Otázky na skúšku

Udalosť. Operácie s náhodnými udalosťami.

Pojem pravdepodobnosti udalosti.

Pravidlá sčítania a násobenia pravdepodobností. Podmienené pravdepodobnosti.

Vzorec úplnej pravdepodobnosti. Bayesov vzorec.

Bernoulliho schéma.

Náhodná veličina, jej distribučná funkcia a distribučné rady.

Základné vlastnosti distribučnej funkcie.

Očakávaná hodnota. Vlastnosti matematického očakávania.

Disperzia. Disperzné vlastnosti.

Hustota rozdelenia pravdepodobnosti jednorozmernej náhodnej premennej.

Typy rozdelení: rovnomerné, exponenciálne, normálne, binomické a Poissonovo rozdelenie.

Lokálne a integrálne Moivre-Laplaceove vety.

Zákon a distribučná funkcia systému dvoch náhodných veličín.

Hustota distribúcie systému dvoch náhodných veličín.

Podmienené zákony rozdelenia, podmienené matematické očakávanie.

Závislé a nezávislé náhodné premenné. Korelačný koeficient.

Ukážka. Spracovanie vzorky. Polygón a frekvenčný histogram. Empirická distribučná funkcia.

Koncept odhadu distribučných parametrov. Požiadavky na hodnotenie. Interval spoľahlivosti. Budovanie intervalov pre odhad matematického očakávania a štandardnej odchýlky.

štatistické hypotézy. Kritériá súhlasu.

V aplikáciách teórie pravdepodobnosti má primárny význam kvantitatívna charakterizácia experimentu. Množstvo, ktoré možno kvantitatívne určiť a ktoré môže v dôsledku experimentu nadobudnúť rôzne hodnoty v závislosti od prípadu, sa nazýva náhodná premenná.

Príklady náhodných premenných:

1. Počet výskytov párneho počtu bodov v desiatich hodoch kockou.

2. Počet zásahov do terča strelcom, ktorý vypáli sériu výstrelov.

3. Počet úlomkov explodujúceho projektilu.

V každom z vyššie uvedených príkladov môže náhodná premenná nadobudnúť iba izolované hodnoty, to znamená hodnoty, ktoré možno vyčísliť pomocou prirodzeného radu čísel.

Takáto náhodná premenná, ktorej možné hodnoty sú samostatné izolované čísla, ktoré táto premenná naberá s určitou pravdepodobnosťou, sa nazýva diskrétne.

Počet možných hodnôt diskrétnej náhodnej premennej môže byť konečný alebo nekonečný (počítateľný).

distribučný zákon Diskrétna náhodná premenná sa nazýva zoznam jej možných hodnôt a ich zodpovedajúcich pravdepodobností. Zákon rozdelenia diskrétnej náhodnej premennej je možné špecifikovať vo forme tabuľky (rad rozdelenia pravdepodobnosti), analyticky a graficky (polygón rozdelenia pravdepodobnosti).

Pri vykonávaní tohto alebo toho experimentu je potrebné vyhodnotiť skúmanú hodnotu "v priemere". Úlohu priemernej hodnoty náhodnej veličiny zohráva číselná charakteristika tzv matematické očakávania, ktorý je definovaný vzorcom

kde X 1 , X 2 ,.. , X n- hodnoty náhodnej premennej X, a p 1 ,p 2 , ... , p n sú pravdepodobnosti týchto hodnôt (všimnite si, že p 1 + p 2 +…+ p n = 1).

Príklad. Streľba sa vykonáva na cieľ (obr. 11).

Zásah v I dáva tri body, v II - dva body, v III - jeden bod. Počet bodov vyradených jednou ranou jedným strelcom má rozdeľovací zákon tvaru

Na porovnanie zručnosti strelcov stačí porovnať priemerné hodnoty dosiahnutých bodov, t.j. matematické očakávania M(X) a M(Y):

M(X) = 1 0,4 + 2  0,2 + 3  0,4 = 2,0,

M(Y) = 1 0,2 + 2  0,5 + 3  0,3 = 2,1.

Druhý strelec dáva v priemere o niečo vyšší počet bodov, t.j. pri opakovanom snímaní poskytne najlepší výsledok.

Všimnite si vlastnosti matematického očakávania:

1. Matematické očakávanie konštantnej hodnoty sa rovná samotnej konštante:

M(C) =C.

2. Matematické očakávanie súčtu náhodných premenných sa rovná súčtu matematických očakávaní pojmov:

M=(X 1 + X 2 +…+ X n)= M(X 1)+ M(X 2)+…+ M(X n).

3. Matematické očakávanie súčinu vzájomne nezávislých náhodných premenných sa rovná súčinu matematických očakávaní faktorov.

M(X 1 X 2 … X n) = M(X 1)M(X 2)… M(X n).

4. Matematická negácia binomického rozdelenia sa rovná súčinu počtu pokusov a pravdepodobnosti udalosti, ktorá nastane v jednom pokuse (úloha 4.6).

M(X) = pr.

Posúdiť, ako sa náhodná premenná „v priemere“ odchyľuje od svojho matematického očakávania, t.j. na charakterizáciu šírenia hodnôt náhodnej premennej v teórii pravdepodobnosti sa používa pojem disperzia.

disperzia náhodná premenná X sa nazýva matematické očakávanie druhej mocniny odchýlky:

D(X) = M[(X - M(X)) 2 ].

Disperzia je numerická charakteristika disperzie náhodnej premennej. Z definície je zrejmé, že čím menší je rozptyl náhodnej premennej, tým bližšie sa jej možné hodnoty nachádzajú okolo matematického očakávania, to znamená, že čím lepšie sú hodnoty náhodnej premennej charakterizované jej matematickou očakávanie.

Z definície vyplýva, že rozptyl je možné vypočítať podľa vzorca

.

Je vhodné vypočítať disperziu pomocou iného vzorca:

D(X) = M(X 2) - (M(X)) 2 .

Disperzia má nasledujúce vlastnosti:

1. Disperzia konštanty je nulová:

D(C) = 0.

2. Konštantný faktor možno zo znamienka disperzie odstrániť jeho umocnením:

D(CX) = C 2 D(X).

3. Rozptyl súčtu nezávislých náhodných premenných sa rovná súčtu rozptylu členov:

D(X 1 + X 2 + X 3 +…+ X n)= D(X 1)+ D(X 2)+…+ D(X n)

4. Rozptyl binomického rozdelenia sa rovná súčinu počtu pokusov a pravdepodobnosti výskytu a neprítomnosti udalosti v jednom pokuse:

D(X) = npq.

V teórii pravdepodobnosti sa často používa číselná charakteristika, ktorá sa rovná druhej odmocnine rozptylu náhodnej premennej. Táto číselná charakteristika sa nazýva štandardná odchýlka a označuje sa symbolom

.

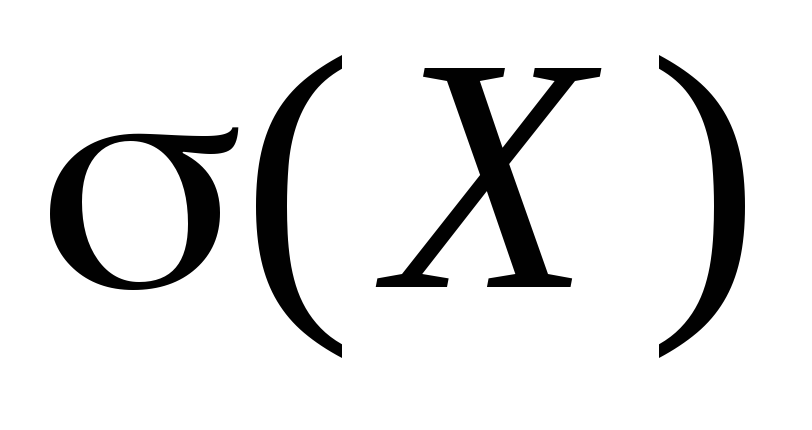Charakterizuje približnú veľkosť odchýlky náhodnej veličiny od jej strednej hodnoty a má rovnaký rozmer ako náhodná veličina.

4.1. Strelec vypáli na cieľ tri rany. Pravdepodobnosť zasiahnutia cieľa pri každom výstrele je 0,3.

Vytvorte distribučný rad počtu prístupov.

Riešenie. Počet zásahov je diskrétna náhodná premenná X. Každá hodnota X n náhodná premenná X zodpovedá určitej pravdepodobnosti P n .

Distribučný zákon diskrétnej náhodnej premennej v tomto prípade možno nastaviť blízko distribúcie.

V tejto úlohe X nadobúda hodnoty 0, 1, 2, 3. Podľa Bernoulliho vzorca

,

nájdite pravdepodobnosť možných hodnôt náhodnej premennej:

R 3 (0) = (0,7) 3 = 0,343,

R 3 (1) =0,3(0,7) 2 = 0,441,

R 3 (2) =(0,3) 2 0,7 = 0,189,

R 3 (3) = (0,3) 3 = 0,027.

Po usporiadaní hodnôt náhodnej premennej X vo vzostupnom poradí dostaneme distribučnú sériu:

X n

Všimnite si, že súčet

znamená pravdepodobnosť, že náhodná premenná X bude mať aspoň jednu hodnotu spomedzi možných, a preto je táto udalosť istá

.

4.2 .V urne sú štyri loptičky, očíslované od 1 do 4. Vyberú sa dve loptičky. Náhodná hodnota X je súčet čísel guľôčok. Zostrojte distribučný rad náhodnej premennej X.

Riešenie. Hodnoty náhodnej premennej X sú 3, 4, 5, 6, 7. Nájdite zodpovedajúce pravdepodobnosti. Hodnota 3 náhodná premenná X môže prijať v jedinom prípade, keď jedna z vybraných loptičiek má číslo 1 a druhá 2. Počet možných výsledkov testu sa rovná počtu kombinácií štyri (počet možných párov loptičiek) po dvoch.

Podľa klasického pravdepodobnostného vzorca dostaneme

podobne,

R(X= 4) =R(X= 6) =R(X= 7) = 1/6.

Súčet 5 sa môže objaviť v dvoch prípadoch: 1 + 4 a 2 + 3, takže

.

X vyzerá ako:

Funkcia nájsť distribúciu F(X) náhodná premenná X a naplánovať to. Vypočítajte pre X jeho matematické očakávanie a rozptyl.

Riešenie. Distribučný zákon náhodnej premennej môže byť daný distribučnou funkciou

F(X) = P(X X).

distribučná funkcia F(X) je neklesajúca, vľavo spojitá funkcia definovaná na celej reálnej osi, pričom

F (- )= 0,F (+ )= 1.

Pre diskrétnu náhodnú premennú je táto funkcia vyjadrená vzorcom

.

Preto v tomto prípade

Graf distribučnej funkcie F(X) je stupňovitá čiara (obr. 12)

	F(X)

Očakávaná hodnotaM(X) je vážený priemer hodnôt X 1 , X 2 ,……X n náhodná premenná X so závažiami ρ 1, ρ 2, …… , ρ n a nazýva sa stredná hodnota náhodnej premennej X. Podľa vzorca

M(X)= x 1 ρ 1 + x 2 ρ 2 + ……+ x n ρ n

M(X) = 3 0,14 + 5 0,2 + 7 0,49 + 11 0,17 = 6,72.

Disperzia charakterizuje stupeň rozptylu hodnôt náhodnej premennej od jej priemernej hodnoty a označuje sa D(X):

D(X)=M[(HM(X)) 2 ]= M(X 2) –[M(X)] 2 .

Pre diskrétnu náhodnú premennú má rozptyl tvar

alebo sa dá vypočítať podľa vzorca

Nahradením číselných údajov problému do vzorca dostaneme:

M(X 2) = 3 2 ∙ 0,14+5 2 ∙ 0,2+7 2 ∙ 0,49+11 2 ∙ 0,17 = 50,84

D(X) = 50,84-6,72 2 = 5,6816.

4.4. Dve kocky sa hádžu dvakrát súčasne. Napíšte zákon binomického rozdelenia pre diskrétnu náhodnú premennú X- počet výskytov párneho celkového počtu bodov na dvoch kockách.

Riešenie. Zoberme do úvahy náhodnú udalosť

ALE= (na dvoch kockách v jednom hode padol celkovo párny počet bodov).

Pomocou klasickej definície pravdepodobnosti nájdeme

R(ALE)= ,

kde n - počet možných výsledkov testu sa zistí pravidlom

násobenia:

n = 6∙6 =36,

m - počet priaznivých udalostí ALE výsledky - rovnaké

m= 3∙6=18.

Pravdepodobnosť úspechu v jednom pokuse je teda

ρ = P(ALE)= 1/2.

Problém je vyriešený pomocou Bernoulliho testovacej schémy. Jednou z výziev je hodiť raz dvoma kockami. Počet takýchto testov n = 2. Náhodná veličina X nadobúda hodnoty 0, 1, 2 s pravdepodobnosťou

R 2 (0) =,R 2 (1) =∙,R 2 (2) =

Požadované binomické rozdelenie náhodnej premennej X môže byť reprezentovaná ako distribučná séria:

X n
ρ n

4.5 . V sérii šiestich dielov sú štyri štandardné diely. Náhodne boli vybrané tri položky. Zostavte rozdelenie pravdepodobnosti diskrétnej náhodnej premennej X- počet normovaných častí medzi vybranými a nájsť ich matematické očakávanie.

Riešenie. Hodnoty náhodnej premennej X sú čísla 0,1,2,3. To je jasné R(X=0)=0, keďže existujú len dve neštandardné časti.

R(X=1) =
=1/5,

R(X= 2) =
= 3/5,

R(X=3) =
= 1/5.

Zákon distribúcie náhodnej premennej X reprezentovať ako distribučný rad:

X n
ρ n

Očakávaná hodnota

M(X)=1 ∙ 1/5+2 ∙ 3/5+3 ∙ 1/5=2.

4.6 . Dokážte, že matematické očakávanie diskrétnej náhodnej premennej X- počet výskytov udalosti ALE v n nezávislé testy, v každom z nich sa pravdepodobnosť výskytu udalosti rovná ρ - sa rovná súčinu počtu pokusov pravdepodobnosti udalosti vyskytujúcej sa v jednom pokuse, to znamená dokázať, že matematické očakávanie binomického rozdelenia

M(X) =n . ρ ,

zatiaľ čo rozptyl

D(X) =np .

Riešenie. Náhodná hodnota X môže nadobúdať hodnoty 0, 1, 2…, n. Pravdepodobnosť R(X= k) sa nachádza podľa Bernoulliho vzorca:

R(X=k)= R n(k)= ρ do (1-ρ ) n- do

Náhodné premenné distribučné rady X vyzerá ako:

X n
ρ n	q n	ρq n- 1	ρq n- 2		ρ n

kde q= 1- ρ .

Pre matematické očakávanie máme výraz:

M(X)=ρq n - 1 +2 ρ 2 q n - 2 +…+.n ρ n

V prípade jedného testu, teda s n= 1 pre náhodnú premennú X 1 - počet výskytov udalosti ALE- distribučná séria má tvar:

X n
ρ n

M(X 1)= 0 q + 1 ∙ p = p

D(X 1) = p – p 2 = p(1- p) = pq.

Ak X k - počet výskytov udalosti ALE v ktorom teste teda R(X do)= ρ a

X=X 1 +X 2 +….+X n .

Odtiaľto sa dostaneme

M(X)=M(X 1 )+M(X 2)+ … +M(X n)= nρ,

D(X)=D(X 1)+D(X 2)+ ... +D(X n)=npq.

4.7. QCD kontroluje produkty z hľadiska štandardizácie. Pravdepodobnosť, že položka je štandardná, je 0,9. Každá dávka obsahuje 5 kusov. Nájdite matematické očakávanie diskrétnej náhodnej premennej X- počet šarží, z ktorých každá sa bude rovnať 4 štandardným výrobkom - ak 50 šarží podlieha overeniu.

Riešenie. Pravdepodobnosť, že v každej náhodne vybranej šarži budú 4 štandardné položky, je konštantná; označme to tým ρ .Potom matematické očakávanie náhodnej premennej X rovná sa M(X)= 50∙ρ.

Poďme nájsť pravdepodobnosť ρ podľa Bernoulliho vzorca:

ρ=P 5 (4)== 0,94∙0,1=0,32.

M(X)= 50∙0,32=16.

4.8 . Hodia sa tri kocky. Nájdite matematické očakávanie súčtu stratených bodov.

Riešenie. Môžete nájsť rozdelenie náhodnej premennej X- súčet vypadnutých bodov a následne jeho matematické očakávanie. Tento spôsob je však príliš ťažkopádny. Jednoduchšie je použiť iný trik, reprezentujúci náhodnú premennú X, ktorého matematické očakávanie sa má vypočítať, ako súčet niekoľkých jednoduchších náhodných veličín, ktorých matematické očakávanie je jednoduchšie vypočítať. Ak náhodná premenná X i je počet získaných bodov i– kosti ( i= 1, 2, 3), potom súčet bodov X vyjadrené vo forme

X = X 1 + X 2 + X 3 .

Na výpočet matematického očakávania pôvodnej náhodnej premennej zostáva len použiť vlastnosť matematického očakávania

M(X 1 + X 2 + X 3 )= M(X 1 )+ M(X 2)+ M(X 3 ).

To je zrejmé

R(X i = K)= 1/6, TO= 1, 2, 3, 4, 5, 6, i= 1, 2, 3.

Preto matematické očakávanie náhodnej premennej X i má formu

M(X i) = 1/6∙1 + 1/6∙2 +1/6∙3 + 1/6∙4 + 1/6∙5 + 1/6∙6 = 7/2,

M(X) = 3∙7/2 = 10,5.

4.9. Určte matematické očakávanie počtu zariadení, ktoré počas testu zlyhali, ak:

a) pravdepodobnosť zlyhania všetkých zariadení je rovnaká R a počet testovaných zariadení sa rovná n;

b) pravdepodobnosť zlyhania pre i – nástroj sa rovná p i , i= 1, 2, … , n.

Riešenie. Nech náhodná premenná X je potom počet zlyhaných zariadení

X = X 1 + X 2 + … + X n ,

X i =

To je jasné

R(X i = 1)= R i , R(X i = 0)= 1– R i ,i= 1, 2, … ,n.

M(X i)= 1∙R i + 0∙(1-R i)=P i ,

M(X)=M(X 1)+M(X 2)+ … +M(X n)=P 1 +P 2 + ... + P n .

V prípade „a“ je pravdepodobnosť poruchy zariadenia rovnaká, t.j.

R i =p,i= 1, 2, … ,n.

M(X)= np.

Táto odpoveď by sa dala získať okamžite, keby sme si všimli, že náhodná premenná X má binomické rozdelenie s parametrami ( n, p).

4.10. Dve kocky sa hádžu dvakrát súčasne. Napíšte zákon binomického rozdelenia pre diskrétnu náhodnú premennú X - počet výskytov párneho počtu bodov na dvoch kockách.

Riešenie. Nechaj

ALE=(strata párneho čísla na prvej kocke),

B =(strata párneho čísla na druhej kocke).

Strata párneho čísla na oboch kockách pri jednom hode bude vyjadrená súčinom AB. Potom

R (AB) = R(ALE)∙R(AT) =
.

Výsledok druhého hodu dvoma kockami nezávisí od prvého, takže Bernoulliho vzorec je použiteľný, keď

n = 2,p = 1/4, q = 1– p = 3/4.

Náhodná hodnota X môže nadobúdať hodnoty 0, 1, 2 , pravdepodobnosť, ktorú zistíme podľa Bernoulliho vzorca:

R(X= 0)= P 2 (0) = q 2 = 9/16,

R(X= 1)= P 2 (1)= C ,R∙q = 6/16,

R(X= 2)= P 2 (2)= C , R 2 = 1/16.

Náhodné premenné distribučné rady X:

4.11. Zariadenie pozostáva z veľkého počtu samostatne fungujúcich prvkov s rovnako veľmi malou pravdepodobnosťou zlyhania každého prvku v priebehu času. t. Zistite priemerný počet zlyhaní v priebehu času t prvkov, ak je pravdepodobnosť, že aspoň jeden prvok počas tejto doby zlyhá, 0,98.

Riešenie. Počet zlyhaní v priebehu času t prvky - náhodná premenná X, ktorý je rozdelený podľa Poissonovho zákona, keďže počet prvkov je veľký, prvky pracujú nezávisle a pravdepodobnosť zlyhania každého prvku je malá. Priemerný počet výskytov udalosti v n skúšky rovná sa

M(X) = np.

Od pravdepodobnosti zlyhania Komu prvky z n sa vyjadruje vzorcom

R n (Komu)
,

kde  = np, potom pravdepodobnosť, že žiadny prvok v čase nezlyhá t dostaneme sa K = 0:

R n (0)= e -  .

Preto je pravdepodobnosť opačnej udalosti v priebehu času t aspoň jeden prvok zlyhá - rovná sa 1 - napr -  . Podľa stavu úlohy sa táto pravdepodobnosť rovná 0,98. Z rovnice

1 - e -  = 0,98,

e -  = 1 – 0,98 = 0,02,

odtiaľto  = - ln 0,02  4.

Takže na čas t prevádzka zariadenia zlyhá v priemere 4 prvky.

4.12 . Kockou sa hádže, kým nepadne „dvojka“. Nájdite priemerný počet hodov.

Riešenie. Zavádzame náhodnú premennú X- počet testov, ktoré sa musia vykonať, kým nenastane udalosť, ktorá nás zaujíma. Pravdepodobnosť, že X= 1 sa rovná pravdepodobnosti, že pri jednom hode kockou vypadne „dvojka“, t.j.

R(X= 1) = 1/6.

Udalosť X= 2 znamená, že pri prvom pokuse „dvojka“ nevypadla, pri druhom však vypadla. Pravdepodobnosť udalosti X= 2 zistíme pravidlom násobenia pravdepodobnosti nezávislých udalostí:

R(X= 2) = (5/6)∙(1/6)

podobne,

R(X= 3) = (5/6) 2 ∙1/6, R(X= 4) = (5/6) 2 ∙1/6

atď. Získame sériu rozdelení pravdepodobnosti:

					(5/6) do ∙1/6

Priemerný počet hodov (skúšok) je matematické očakávanie

M(X) = 1∙1/6 + 2∙5/6∙1/6 + 3∙(5/6) 2 ∙1/6 + … + Komu (5/6) Komu -1 ∙1/6 + … =

1/6∙(1+2∙5/6 +3∙(5/6) 2 + … + Komu (5/6) Komu -1 + …)

Poďme nájsť súčet série:

Komug Komu -1 = (g Komu) g 
.

v dôsledku toho

M(X) = (1/6) (1/ (1 – 5/6) 2 = 6.

Preto je potrebné vykonať v priemere 6 hodov kockou, kým nevypadne „dvojka“.

4.13. Nezávislé testy sa vykonávajú s rovnakou pravdepodobnosťou výskytu udalosti ALE v každom teste. Nájdite pravdepodobnosť výskytu udalosti ALE ak je rozptyl počtu výskytov udalosti v troch nezávislých pokusoch 0,63 .

Riešenie. Počet výskytov udalosti v troch pokusoch je náhodná premenná X rozdelené podľa binomického zákona. Rozptyl počtu výskytov udalosti v nezávislých pokusoch (s rovnakou pravdepodobnosťou výskytu udalosti v každom pokuse) sa rovná súčinu počtu pokusov a pravdepodobnosti výskytu a neexistencie udalosti ( úloha 4.6)

D(X) = npq.

Podľa podmienok n = 3, D(X) = 0,63, takže môžete R nájsť z rovnice

0,63 = 3∙R(1-R),

ktorý má dve riešenia R 1 = 0,7 a R 2 = 0,3.