Pozoruhodná teória limitov. Prvá a druhá úžasná hranica

Pojem „pozoruhodný limit“ je široko používaný v učebniciach a metodické príručky na označenie dôležitých identít, ktoré výrazne pomáhajú zjednodušiť si prácu o hľadaní hraníc.

Ale môcť priniesť svoju hranicu až po pozoruhodné, treba sa na to dobre pozrieť, pretože sa nenachádzajú v priamej forme, ale často vo forme dôsledkov, vybavené dodatočnými termínmi a faktormi. Najprv však teória, potom príklady a uspejete!

Prvá úžasná limitka

Páčilo sa? Pridať do záložiek

Prvá pozoruhodná hranica je napísaná takto (neistota tvaru $0/0$):

$$ \lim\limits_(x\to 0)\frac(\sin x)(x)=1. $$

Dôsledky prvého pozoruhodného limitu

$$ \lim\limits_(x\to 0)\frac(x)(\sin x)=1. $$ $$ \lim\limits_(x\to 0)\frac(\sin (ax))(\sin (bx))=\frac(a)(b). $$ $$ \lim\limits_(x\to 0)\frac(\tan x)(x)=1. $$ $$ \lim\limits_(x\to 0)\frac(\arcsin x)(x)=1. $$ $$ \lim\limits_(x\to 0)\frac(\arctan x)(x)=1. $$ $$ \lim\limits_(x\to 0)\frac(1-\cos x)(x^2/2)=1. $$

Príklady riešení: 1 úžasná limita

Príklad 1 Vypočítajte limit $$\lim\limits_(x\to 0)\frac(\sin 3x)(8x).$$

Riešenie. Prvý krok je vždy rovnaký - do funkcie dosadíme limitnú hodnotu $x=0$ a dostaneme:

$$\left[ \frac(\sin 0)(0) \right] = \left[\frac(0)(0)\right].$$

Získali sme neistotu tvaru $\left[\frac(0)(0)\right]$, ktorá by mala byť zverejnená. Ak sa pozriete pozorne, pôvodný limit je veľmi podobný prvému pozoruhodnému, ale nie je rovnaký. Našou úlohou je priviesť to k podobnosti. Transformujme to takto - pozrite sa na výraz pod sínusom, urobte to isté v menovateli (relatívne povedané, vynásobte a vydeľte $3x$), potom zredukujte a zjednodušte:

$$ \lim\limits_(x\to 0)\frac(\sin 3x)(8x) = \lim\limits_(x\to 0)\frac(\sin 3x)(3x)\frac(3x)(8x )=\lim\limits_(x\to 0)\frac(\sin (3x))(3x)\frac(3)(8)=\frac(3)(8). $$

Vyššie je presne prvý pozoruhodný limit: $$ \lim\limits_(x\to 0)\frac(\sin (3x))(3x) = \lim\limits_(y\to 0)\frac(\sin ( y ))(y)=1, \text( vykonalo podmienené nahradenie ) y=3x. $$ odpoveď: $3/8$.

Príklad 2 Vypočítajte limit $$\lim\limits_(x\to 0)\frac(1-\cos 3x)(\tan 2x\cdot \sin 4x).$$

Riešenie. Do funkcie dosadíme limitnú hodnotu $x=0$ a dostaneme:

$$\left[ \frac(1-\cos 0)(\tan 0\cdot \sin 0)\right] =\left[ \frac(1-1)( 0\cdot 0)\right] = \left [\frac(0)(0)\right].$$

Získali sme neistotu tvaru $\left[\frac(0)(0)\right]$. Poďme transformovať limit pomocou prvého úžasného limitu (trikrát!) pre zjednodušenie:

$$\lim\limits_(x\to 0)\frac(1-\cos 3x)(\tan 2x\cdot \sin 4x) = \lim\limits_(x\to 0)\frac( 2 \sin^2 (3x/2))(\sin 2x\cdot \sin 4x)\cdot \cos 2x = $$ $$ = 2\lim\limits_(x\to 0)\frac( \sin^2 (3x/2) )((3x/2)^2) \cdot \frac( 2x)(\sin 2x) \cdot \frac( 4x)( \sin 4x)\cdot \frac( (3x/2)^2)( 2x \ cdot 4x) \cdot \cos 2x = $$ $$ =2\lim\limits_(x\to 0) 1 \cdot 1 \cdot 1 \cdot \frac( (9/4)x^2)( 8x^2 ) \cdot \cos 2x= 2 \cdot \frac( 9)( 32) \lim\limits_(x\to 0) \cos 2x=\frac(9)(16). $$

odpoveď: $9/16$.

Príklad 3 Nájdite limit $$\lim\limits_(x\to 0)\frac(\sin (2x^3+3x))(5x-x^5).$$

Riešenie.Čo ak je pod goniometrickou funkciou zložitý výraz? Nevadí, tu postupujeme rovnako. Najprv skontrolujeme typ neistoty, dosadíme $x=0$ do funkcie a získame:

$$\left[ \frac(\sin (0+0))(0-0)\right] = \left[\frac(0)(0)\right].$$

Získali sme neistotu tvaru $\left[\frac(0)(0)\right]$. Vynásobte a vydeľte $2x^3+3x$:

$$ \lim\limits_(x\to 0)\frac(\sin (2x^3+3x))(5x-x^5)=\lim\limits_(x\to 0)\frac(\sin (2x ^3+3x))((2x^3+3x)) \cdot \frac(2x^3+3x)(5x-x^5)=\lim\limits_(x\to 0) 1 \cdot \frac( 2x^3+3x)(5x-x^5)= \vľavo[\frac(0)(0)\vpravo] = $$

Opäť sme dostali neistotu, ale v tomto prípade je to len zlomok. Znížime čitateľa a menovateľa o $x$:

$$ =\lim\limits_(x\to 0) \frac(2x^2+3)(5-x^4)= \left[\frac(0+3)(5-0)\right] =\ frac(3)(5). $$

odpoveď: $3/5$.

Druhá úžasná limitka

Druhá pozoruhodná hranica je napísaná takto (neistota tvaru $1^\infty$):

$$ \lim\limits_(x\to \infty) \left(1+\frac(1)(x)\right)^(x)=e, \quad \text(alebo) \quad \lim\limits_( x\do 0) \vľavo(1+x\vpravo)^(1/x)=e. $$

Dôsledky druhého pozoruhodného limitu

$$ \lim\limits_(x\to \infty) \left(1+\frac(a)(x)\right)^(bx)=e^(ab). $$ $$ \lim\limits_(x\to 0)\frac(\ln (1+x))(x)=1. $$ $$ \lim\limits_(x\to 0)\frac(e^x -1)(x)=1. $$ $$ \lim\limits_(x\to 0)\frac(a^x-1)(x \ln a)=1, a>0, \ne 1. $$ $$ \lim\limits_( x\to 0)\frac((1+x)^(a)-1)(ax)=1. $$

Príklady riešení: 2 nádherné limity

Príklad 4. Nájdite limit $$\lim\limits_(x\to \infty)\left(1-\frac(2)(3x)\right)^(x+3).$$

Riešenie. Skontrolujeme typ neistoty, dosadíme $x=\infty$ do funkcie a získame:

$$\left[ \left(1-\frac(2)(\infty)\right)^(\infty) \right] = \left.$$

Získali sme neistotu tvaru $\left$. Limit možno zredukovať na druhú pozoruhodnú vec. Poďme sa transformovať:

$$ \lim\limits_(x\to \infty)\left(1-\frac(2)(3x)\right)^(x+3) = \lim\limits_(x\to \infty)\left( 1+\frac(1)((-3x/2))\vpravo)^(\frac(-3x/2)(-3x/2)(x+3))= $$ $$ = \lim\limits_ (x\to \infty)\vľavo(\vľavo(1+\frac(1)((-3x/2))\vpravo)^((-3x/2))\vpravo)^\frac(x+3 )(-3x/2)= $$

Výraz v zátvorkách je vlastne druhá pozoruhodná hranica $\lim\limits_(t\to \infty) \left(1+\frac(1)(t)\right)^(t)=e$, len $t= - 3x/2 doláre, takže

$$ = \lim\limits_(x\to \infty)\left(e\right)^\frac(x+3)(-3x/2)= \lim\limits_(x\to \infty)e^\ frac(1+3/x)(-3/2)=e^(-2/3). $$

odpoveď:$e^(-2/3)$.

Príklad 5. Nájdite limit $$\lim\limits_(x\to \infty)\left(\frac(x^3+2x^2+1)(x^3+x-7)\right)^(x).$ $

Riešenie. Do funkcie dosadíme $x=\infty$ a získame neistotu tvaru $\left[ \frac(\infty)(\infty)\right]$. A potrebujeme $\left$. Začnime teda transformáciou výrazu v zátvorkách:

$$ \lim\limits_(x\to \infty)\left(\frac(x^3+2x^2+1)(x^3+x-7)\right)^(x) = \lim\limits_ (x\to \infty)\vľavo(\frac(x^3+(x-7)-(x-7)+2x^2+1)(x^3+x-7)\vpravo)^(x ) = \lim\limits_(x\to \infty)\left(\frac((x^3+x-7)+(-x+7+2x^2+1))(x^3+x-7 )\vpravo)^(x) = $$ $$ = \lim\limits_(x\to \infty)\vľavo(1+\frac(2x^2-x+8)(x^3+x-7) \right)^(x) = \lim\limits_(x\to \infty)\left(\left(1+\frac(2x^2-x+8)(x^3+x-7)\vpravo) ^(\frac(x^3+x-7)(2x^2-x+8))\right)^(x \frac(2x^2-x+8)(x^3+x-7)) = $$

Výraz v zátvorkách je vlastne druhá pozoruhodná hranica $\lim\limits_(t\to \infty) \left(1+\frac(1)(t)\right)^(t)=e$, len $t= \ frac(x^3+x-7)(2x^2-x+8) \to \infty$, preto

$$ = \lim\limits_(x\to \infty)\left(e\right)^(x \frac(2x^2-x+8)(x^3+x-7))= \lim\limits_ (x\to \infty)e^( \frac(2x^2-x+8)(x^2+1-7/x))= \lim\limits_(x\to \infty)e^( \frac (2-1/x+8/x^2)(1+1/x^2-7/x^3))=e^(2). $$

Tento článok: „Druhá pozoruhodná hranica“ je venovaný zverejneniu v medziach neistoty formulára:

$ \bigg[\frac(\infty)(\infty)\bigg]^\infty $ a $ ^\infty $.

Takéto neistoty možno odhaliť aj pomocou logaritmu exponenciálnej funkcie, ale toto je iná metóda riešenia, ktorej sa budeme venovať v inom článku.

Vzorec a dôsledky

Vzorec druhá pozoruhodná hranica je napísaná takto: $$ \lim_(x \to \infty) \bigg (1+\frac(1)(x)\bigg)^x = e, \text( kde ) e \cca 2,718 $$

Vyplýva to zo vzorca dôsledky, ktoré sú veľmi vhodné na riešenie príkladov s limitami: $$ \lim_(x \to \infty) \bigg (1 + \frac(k)(x) \bigg)^x = e^k, \text( kde ) k \in \mathbb(R) $$ $$ \lim_(x \to \infty) \bigg (1 + \frac(1)(f(x)) \bigg)^(f(x)) = e $ $ $$ \lim_(x \to 0) \bigg (1 + x \bigg)^\frac(1)(x) = e $$

Stojí za zmienku, že druhú pozoruhodnú hranicu nemožno vždy použiť na exponenciálnu funkciu, ale iba v prípadoch, keď má základňa tendenciu k jednote. Ak to chcete urobiť, najprv mentálne vypočítajte hranicu základne a potom vyvodte závery. To všetko bude diskutované v príkladoch riešení.

Príklady riešení

Pozrime sa na príklady riešení pomocou priameho vzorca a jeho dôsledky. Budeme tiež analyzovať prípady, v ktorých vzorec nie je potrebný. Stačí napísať iba hotovú odpoveď.

Príklad 1

Nájdite limit $ \lim_(x\to\infty) \bigg(\frac(x+4)(x+3) \bigg)^(x+3) $

Riešenie

Dosaďme do limity nekonečno a pozrime sa na neistotu: $$ \lim_(x\to\infty) \bigg(\frac(x+4)(x+3) \bigg)^(x+3) = \bigg (\frac (\infty)(\infty)\bigg)^\infty $$ Nájdime hranicu základne: $$ \lim_(x\to\infty) \frac(x+4)(x+3)= \lim_(x\to\infty) \frac(x(1+\frac) (4)() x)))(x(1+\frac(3)(x))) = 1 $$ Získali sme základ rovný jednej, čo znamená, že už môžeme aplikovať druhú pozoruhodnú hranicu. Ak to chcete urobiť, upravte základ funkcie na vzorec odčítaním a pridaním jedného: $$ \lim_(x\to\infty) \bigg(1 + \frac(x+4)(x+3) - 1 \bigg)^(x+3) = \lim_(x\to\infty) \ bigg(1 + \frac(1)(x+3) \bigg)^(x+3) = $$ Pozrime sa na druhý dôsledok a zapíšme si odpoveď: $$ \lim_(x\to\infty) \bigg(1 + \frac(1)(x+3) \bigg)^(x+3) = e $$ Ak nemôžete vyriešiť svoj problém, pošlite nám ho. My zabezpečíme podrobné riešenie. Budete si môcť pozrieť priebeh výpočtu a získať informácie. Pomôže vám to získať známku od učiteľa včas!

Odpoveď

$$ \lim_(x\to\infty) \bigg(1 + \frac(1)(x+3) \bigg)^(x+3) = e $$

Príklad 4

Vyriešte limit $ \lim_(x\to \infty) \bigg (\frac(3x^2+4)(3x^2-2) \bigg) ^(3x) $

Riešenie

Nájdeme hranicu základne a vidíme, že $ \lim_(x\to\infty) \frac(3x^2+4)(3x^2-2) = 1 $, čo znamená, že môžeme použiť druhú pozoruhodnú hranicu. Podľa štandardného plánu pridávame a odčítame jeden od základu stupňa: $$ \lim_(x\to \infty) \bigg (1+\frac(3x^2+4)(3x^2-2)-1 \bigg) ^(3x) = \lim_(x\to \infty ) \bigg (1+\frac(6)(3x^2-2) \bigg) ^(3x) = $$ Zlomok upravíme na vzorec 2. noty. limit: $$ = \lim_(x\to \infty) \bigg (1+\frac(1)(\frac(3x^2-2)(6)) \bigg) ^(3x) = $$ Teraz upravíme stupeň. Mocnina musí obsahovať zlomok rovný menovateľovi základu $ \frac(3x^2-2)(6) $. Ak to chcete urobiť, vynásobte a vydeľte ním stupeň a pokračujte v riešení: $$ = \lim_(x\to \infty) \bigg (1+\frac(1)(\frac(3x^2-2)(6)) \bigg) ^(\frac(3x^2-2) (6) \cdot \frac(6)(3x^2-2)\cdot 3x) = \lim_(x\to \infty) e^(\frac(18x)(3x^2-2)) = $$ Limit umiestnený v mocnine na $ e $ sa rovná: $ \lim_(x\to \infty) \frac(18x)(3x^2-2) = 0 $. Preto pokračujeme v riešení, ktoré máme:

Odpoveď

$$ \lim_(x\to \infty) \bigg (\frac(3x^2+4)(3x^2-2) \bigg) ^(3x) = 1 $$

Pozrime sa na prípady, keď je problém podobný druhej pozoruhodnej hranici, ale dá sa vyriešiť aj bez nej.

V článku „Druhá pozoruhodná hranica: príklady riešení“ bol analyzovaný a uvedený vzorec a jeho dôsledky bežné typy problémy na túto tému.

Nájdite úžasné limityŤažké to majú nielen mnohí študenti prvého a druhého ročníka, ktorí teóriu limitov študujú, ale aj niektorí učitelia.

Vzorec pre prvý pozoruhodný limit

Dôsledky prvého pozoruhodného limitu napíšeme to do vzorcov
1. 2. 3. 4. Ale po svojom všeobecné vzorce pozoruhodné limity nikomu nepomôžu pri skúške alebo teste. Ide o to, že skutočné úlohy skonštruované tak, že stále potrebujeme dospieť k vyššie napísaným vzorcom. A väčšina študentov, ktorí vymeškajú hodiny, študujú tento kurz v neprítomnosti alebo majú učiteľov, ktorí sami nie vždy rozumejú tomu, čo vysvetľujú, nedokáže vypočítať tie najzákladnejšie príklady do pozoruhodných hraníc. Zo vzorcov prvej pozoruhodnej limity vidíme, že s ich pomocou je možné študovať neistoty typu nula delená nulou pre výrazy s goniometrickými funkciami. Uvažujme najprv o niekoľkých príkladoch prvej pozoruhodnej limity a potom študujme druhú pozoruhodnú limitu.

Príklad 1. Nájdite limitu funkcie sin(7*x)/(5*x)
Riešenie: Ako vidíte, funkcia pod limitou je blízko prvej pozoruhodnej limity, ale limita samotnej funkcie sa rozhodne nerovná jednej. V tomto druhu úloh o limitách by sme mali vybrať v menovateli premennú s rovnakým koeficientom, aký obsahuje premenná pod sínusom. V tomto prípade vydeľte a vynásobte číslom 7

Niekomu sa takýto detail bude zdať zbytočný, no väčšine študentov, ktorí majú problém s limitmi, to pomôže lepšie pochopiť pravidlá a zvládnuť teoretickú látku.
Tiež, ak existuje spätný pohľad funkcie je tiež prvým pozoruhodným limitom. A to všetko preto, že úžasný limit sa rovná jednej

Rovnaké pravidlo platí pre dôsledky 1. pozoruhodnej hranice. Preto, ak sa vás opýtajú: "Aký je prvý pozoruhodný limit?" Bez váhania by ste mali odpovedať, že je to jednotka.

Príklad 2. Nájdite limitu funkcie sin(6x)/tan(11x)
Riešenie: Aby sme pochopili konečný výsledok, napíšme funkciu do formulára

Ak chcete použiť pravidlá pozoruhodnej hranice, násobte a delte podľa faktorov

Ďalej napíšeme limitu súčinu funkcií cez súčin limity

Bez zložitých vzorcov sme našli limitu goniometrických funkcií. Aby ste zvládli jednoduché vzorce, skúste vymyslieť a nájsť hranicu 2 a 4, vzorec pre dôsledok 1 nádhernej hranice. Pozrieme sa na zložitejšie problémy.

Príklad 3: Vypočítajte limit (1-cos(x))/x^2
Riešenie: Pri kontrole substitúciou dostaneme neistotu 0/0. Mnoho ľudí nevie, ako zredukovať takýto príklad na jednu pozoruhodnú hranicu. Tu by sa mal použiť trigonometrický vzorec

V tomto prípade sa limit premení na jasnú formu

Funkciu sa nám podarilo zredukovať na druhú mocninu pozoruhodného limitu.

Príklad 4. Nájdite limitu
Riešenie: Pri dosadzovaní dostaneme známu vlastnosť 0/0. Premenná však má skôr tendenciu k Pi ako k nule. Preto, aby sme použili prvú pozoruhodnú limitu, vykonáme takú zmenu v premennej x, aby sa nová premenná dostala na nulu. Aby sme to dosiahli, označíme menovateľa ako novú premennú Pi-x=y

Pomocou trigonometrického vzorca uvedeného v predchádzajúcej úlohe sa teda príklad zredukuje na 1 pozoruhodnú hranicu.

Príklad 5: Výpočet limitu
Riešenie: Spočiatku nie je jasné, ako limity zjednodušiť. Ale keďže existuje príklad, musí existovať aj odpoveď. Skutočnosť, že premenná ide do jednoty, dáva pri dosadzovaní vlastnosť tvaru nula vynásobená nekonečnom, takže dotyčnica musí byť nahradená pomocou vzorca

Potom dostaneme požadovanú neistotu 0/0. Ďalej vykonáme zmenu premenných v limite a použijeme periodicitu kotangens

Posledné substitúcie nám umožňujú použiť Dôsledok 1 pozoruhodného limitu.

Druhá pozoruhodná hranica sa rovná exponenciáli

Toto je klasika, ktorú nie je vždy ľahké dosiahnuť v skutočných limitných problémoch.
Vo výpočtoch budete potrebovať limity sú dôsledkom druhého pozoruhodného limitu:
1. 2. 3. 4.
Vďaka druhej pozoruhodnej hranici a jej dôsledkom je možné skúmať neistoty ako nula delená nulou, jedna mocninou nekonečna a nekonečno delené nekonečnom, a to dokonca v rovnakej miere.

Začnime sa zoznamovať jednoduché príklady.

Príklad 6. Nájdite limit funkcie
Riešenie: Priame použitie 2. pozoruhodného limitu nebude fungovať. Najprv by ste mali transformovať exponent tak, aby vyzeral ako inverzia termínu v zátvorkách

Toto je technika redukcie na 2. pozoruhodnú hranicu a v podstate odvodenie 2. vzorca pre dôsledok limity.

Príklad 7. Nájdite limit funkcie
Riešenie: Máme úlohy pre vzorec 3 z 2. dôsledku nádhernej limity. Nahradením nuly získame singularitu tvaru 0/0. Aby sme zvýšili limit na pravidlo, otočíme menovateľa tak, aby premenná mala rovnaký koeficient ako v logaritme

Je tiež ľahké pochopiť a vykonať skúšku. Ťažkosti študentov pri výpočte limitov začínajú nasledujúcimi problémami.

Príklad 8. Vypočítajte limitu funkcie[(x+7)/(x-3)]^(x-2)
Riešenie: Máme singularitu 1. typu na mocninu nekonečna. Ak mi neveríte, môžete všade nahradiť „X“ nekonečno a uistiť sa o tom. Aby sme vytvorili pravidlo, vydelíme čitateľa menovateľom v zátvorkách, aby sme to urobili, najprv vykonáme manipulácie

Dosadíme výraz do limity a premeníme ho na 2 nádherné limity

Limit sa rovná exponenciálnej mocnine 10. Konštanty, ktoré sú výrazmi s premennou, v zátvorkách aj stupňoch, nezavádzajú žiadne „počasie“ - to by ste si mali zapamätať. A ak sa vás učitelia opýtajú: „Prečo neprevediete indikátor?“ (Pre tento príklad v x-3) potom povedzte, že „Keď má premenná tendenciu k nekonečnu, potom k nej dokonca pridajte 100 alebo odčítajte 1000 a limit zostane rovnaký ako predtým!“
Existuje druhý spôsob výpočtu limitov tohto typu. Povieme si o tom v ďalšej úlohe.

Príklad 9. Nájdite hranicu
Riešenie: Teraz vyňame premennú z čitateľa a menovateľa a premeňme jednu vlastnosť na druhú. Na získanie konečnej hodnoty použijeme vzorec Dôsledku 2 pozoruhodnej hranice

Príklad 10. Nájdite limit funkcie
Riešenie: Nie každý môže nájsť daný limit. Ak chcete zvýšiť limit na 2, predstavte si, že sin (3x) je premenná a musíte otočiť exponent

Ďalej zapíšeme indikátor ako mocninu na mocninu


Prechodné argumenty sú popísané v zátvorkách. V dôsledku použitia prvej a druhej pozoruhodnej medze sme získali exponenciálu v kocke.

Príklad 11. Vypočítajte limitu funkcie hriech(2*x)/ln(3*x+1)
Riešenie: Máme neurčitosť tvaru 0/0. Okrem toho vidíme, že funkcia by mala byť prevedená na použitie oboch úžasných limitov. Vykonajte predchádzajúce matematické transformácie

Ďalej, bez problémov, limit nadobudne hodnotu

Takto slobodne sa budete cítiť pri zadaniach, testoch, moduloch, ak sa naučíte rýchlo vypisovať funkcie a zredukovať ich na prvú alebo druhú úžasnú hranicu. Ak je pre vás ťažké zapamätať si dané metódy hľadania limitov, potom sa môžete vždy objednať test na naše limity.
Ak to chcete urobiť, vyplňte formulár, uveďte údaje a priložte súbor s príkladmi. Pomohli sme mnohým študentom – môžeme pomôcť aj vám!

dôkaz:

Dokážme najprv vetu pre prípad postupnosti

Podľa Newtonovho binomického vzorca:

Za predpokladu, že dostaneme

Z tejto rovnosti (1) vyplýva, že ako n rastie, zvyšuje sa počet kladných členov na pravej strane. Okrem toho, ako n rastie, číslo klesá, takže hodnoty pribúdajú. Preto poradie rastúci a (2)*Ukážeme, že je ohraničený. Nahraďte každú zátvorku na pravej strane rovnosti jednou, pravá časť zvyšuje, dostávame nerovnosť

Posilnime výslednú nerovnosť, 3,4,5, ..., stojace v menovateľoch zlomkov, nahraďme číslom 2: V zátvorke nájdeme súčet pomocou vzorca pre súčet členov geometrickej postupnosti: Preto (3)*

Postupnosť je teda ohraničená zhora a nerovnosti (2) a (3) sú splnené: Preto na základe Weierstrassovej vety (kritérium konvergencie postupnosti) postupnosť monotónne rastie a je limitovaný, čo znamená, že má limit, označený písmenom e. Tie.

S vedomím, že druhý pozoruhodný limit platí pre prirodzené hodnoty x, dokážeme druhý pozoruhodný limit pre skutočné x, to znamená, že dokážeme, že . Zoberme si dva prípady:

1. Nech je každá hodnota x uzavretá medzi dve kladné celé čísla: ,kde je celá časť x. => =>

Ak , tak Preto podľa limitu Máme

Na základe kritéria (okolo limity medzifunkcie) existencie limitov

2. Nechajte . Urobme substitúciu − x = t

Z týchto dvoch prípadov vyplýva, že pre skutočné x.

Dôsledky:

9 .) Porovnanie infinitezimálov. Veta o nahradení infinitezimál ekvivalentnými v limite a teoréma o hlavnej časti infinitezimál.

Nech funkcie a( X) a b( X) – b.m. pri X ® X 0 .

DEFINÍCIE.

1)a( X) volal infinitezimálne vyššieho rádu ako b (X) Ak

Napíšte: a( X) = o(b( X)) .

2)a( X) A b( X)sa volajú infinitezimály rovnakého rádu, Ak

kde CÎℝ a C¹ 0 .

Napíšte: a( X) = O(b( X)) .

3)a( X) A b( X) sa volajú ekvivalent , Ak

Napíšte: a( X) ~ b( X).

4)a( X) sa nazýva infinitesimál rádu k relatívny
absolútne nekonečne malé b( X), ak je nekonečne malý a( X)A(b( X)) k mať rovnaké poradie, t.j. Ak

kde CÎℝ a C¹ 0 .

TEOREM 6 (o nahradení infinitezimálov ekvivalentnými).

Nechaj a( X), b( X), 1 ( X), b 1 ( X)– b.m. pri x ® X 0 . Ak a( X) ~ a 1 ( X), b( X) ~ b 1 ( X),

To

Dôkaz: Nechaj ( X) ~ a 1 ( X), b( X) ~ b 1 ( X), Potom

TEOREM 7 (o hlavnej časti nekonečna).

Nechaj a( X)A b( X)– b.m. pri x ® X 0 , a b( X)– b.m. vyššieho rádu ako a( X).

= , a keďže b( X) – vyššieho rádu ako a( X), potom, t.j. od je jasné, že a( X) + b( X) ~ a( X)

10) Spojitosť funkcie v bode (v reči epsilon-delta geometrické limity) Jednostranná spojitosť. Spojitosť na intervale, na segmente. Vlastnosti spojitých funkcií.

1. Základné definície

Nechaj f(X) je definovaný v niektorom okolí bodu X 0 .

DEFINÍCIA 1. Funkcia f(X) volal súvislý v bode X 0 ak je rovnosť pravdivá

Poznámky.

1) Na základe vety 5 §3 môže byť rovnosť (1) napísaná v tvare

Podmienka (2) – definícia kontinuity funkcie v bode v jazyku jednostranné limity .

2) Rovnosť (1) možno napísať aj takto:

Hovoria: „ak je funkcia spojitá v bode X 0, potom je možné zameniť znamienko limity a funkciu."

DEFINÍCIA 2 (v jazyku e-d).

Funkcia f(X) volal súvislý v bode X 0 Ak"e>0 $d>0." taký, Čo

ak xОU( X 0 , d) (t. j. | X – X 0 | < d),

potom f(X)ÎU( f(X 0), e) (t. j. | f(X) – f(X 0) | < e).

Nechaj X, X 0 Î D(f) (X 0 – pevné, X - svojvoľný)

Označme: D X= x – x 0 – prírastok argumentov

D f(X 0) = f(X) – f(X 0) – prírastok funkcie v bodex 0

DEFINÍCIA 3 (geometrická).

Funkcia f(X) zapnuté volal súvislý v bode X 0 ak v tomto bode nekonečne malý prírastok v argumente zodpovedá nekonečne malému prírastku vo funkcii, t.j.

Nechajte funkciu f(X) je definovaný na intervale [ X 0 ; X 0 + d) (na intervale ( X 0 – d; X 0 ]).

DEFINÍCIA. Funkcia f(X) volal súvislý v bode X 0 napravo (vľavo ), ak je rovnosť pravdivá

To je zrejmé f(X) je v bode súvislý X 0 Û f(X) je v bode súvislý X 0 vpravo a vľavo.

DEFINÍCIA. Funkcia f(X) volal nepretržite počas intervalu e ( a; b) ak je spojitý v každom bode tohto intervalu.

Funkcia f(X) sa nazýva spojitý na segmente [a; b] ak je na intervale súvislá (a; b) a má jednosmernú kontinuitu v hraničných bodoch(t. j. kontinuálne v bode a vpravo, v bode b- vľavo).

11) Body zlomu, ich klasifikácia

DEFINÍCIA. Ak funkcia f(X) definované v nejakom okolí bodu x 0 , ale v tomto bode nie je nepretržitý f(X) nazývaný nespojitý v bode x 0 , a samotná pointa X 0 nazývaný bod zlomu funkcie f(X) .

Poznámky.

1) f(X) možno definovať v neúplnom okolí bodu X 0 .

Potom zvážte zodpovedajúcu jednostrannú spojitosť funkcie.

2) Z definície bodu Þ X 0 je bod zlomu funkcie f(X) v dvoch prípadoch:

a) U( X 0, d) О D(f) , ale pre f(X) neplatí rovnosť

b) U * ( X 0, d) О D(f) .

Pre elementárne funkcie možný je len prípad b).

Nechaj X 0 – bod zlomu funkcie f(X) .

DEFINÍCIA. Bod x 0 volal bod zlomu ja druh ak funkcia f(X)má v tomto bode vľavo a vpravo konečné limity.

Ak sú tieto limity rovnaké, potom bod x 0 volal odnímateľný bod zlomu , inak - skokový bod .

DEFINÍCIA. Bod x 0 volal bod zlomu II druh ak je aspoň jedna z jednostranných limitov funkcie f(X)v tomto bode je rovnaký¥ alebo neexistuje.

12) Vlastnosti funkcií spojitých na intervale (Weierstrassova veta (bez dôkazu) a Cauchyho veta

Weierstrassova veta

Nech je funkcia f(x) spojitá na intervale

1)f(x) je obmedzené na

2)f(x) nadobúda najmenšiu hodnotu na intervale a najvyššia hodnota

Definícia: Hodnota funkcie m=f sa nazýva najmenšia, ak m≤f(x) pre ľubovoľné x€ D(f).

Hodnota funkcie m=f sa považuje za najväčšiu, ak m≥f(x) pre ľubovoľné x € D(f).

Funkcia môže nadobudnúť najmenšiu/najväčšiu hodnotu v niekoľkých bodoch segmentu.

f(x3)=f(x4)=max

Cauchyho veta.

Nech je funkcia f(x) spojitá na segmente a x je číslo medzi f(a) a f(b), potom existuje aspoň jeden bod x 0 € taký, že f(x 0)= g

Existuje niekoľko pozoruhodných limitov, ale najznámejšími sú prvý a druhý pozoruhodný limit. Pozoruhodné na týchto limitoch je, že ich majú široké uplatnenie a s ich pomocou možno nájsť ďalšie limity, na ktoré naráža množstvo problémov. To je to, čo urobíme v praktickej časti tejto lekcie. Na vyriešenie problémov ich znížením na prvú alebo druhú pozoruhodnú hranicu nie je potrebné odhaľovať neistoty, ktoré sú v nich obsiahnuté, pretože hodnoty týchto hraníc už dlho odvodili veľkí matematici.

Prvý pozoruhodný limit sa nazýva limita pomeru sínusu nekonečne malého oblúka k rovnakému oblúku, vyjadrená v radiáne:

Prejdime k riešeniu problémov na prvej pozoruhodnej hranici. Poznámka: ak je pod medzným znakom goniometrická funkcia, je to takmer isté znamenie, že tento výraz možno zredukovať na prvú pozoruhodnú medzu.

Príklad 1 Nájdite hranicu.

Riešenie. Namiesto toho náhrada X nula vedie k neistote:

.

Menovateľ je sínus, preto výraz môže byť privedený k prvej pozoruhodnej hranici. Začnime s transformáciou:

.

Menovateľ je sínus troch X, ale čitateľ má iba jedno X, čo znamená, že v čitateli musíte dostať tri X. Prečo? Na predstavenie 3 X = a a získajte výraz.

A dostávame sa k variácii prvého pozoruhodného limitu:

pretože nezáleží na tom, ktoré písmeno (premenná) v tomto vzorci stojí namiesto X.

X vynásobíme tromi a hneď rozdelíme:

.

V súlade s prvým zaznamenaným pozoruhodným limitom nahrádzame zlomkový výraz:

Teraz môžeme konečne vyriešiť tento limit:

.

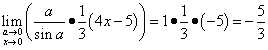Príklad 2 Nájdite hranicu.

Riešenie. Priama substitúcia opäť vedie k neistote „nula delená nulou“:

.

Na získanie prvej pozoruhodnej limity je potrebné, aby x pod sínusovým znamienkom v čitateli a práve x v menovateli mali rovnaký koeficient. Nech sa tento koeficient rovná 2. Aby sme to dosiahli, predstavme si aktuálny koeficient pre x, ako je uvedené nižšie, vykonávaním operácií so zlomkami získame:

.

Príklad 3 Nájdite hranicu.

Riešenie. Pri dosadzovaní opäť dostaneme neistotu „nula delená nulou“:

.

Asi už chápete, že z pôvodného výrazu môžete získať prvú nádhernú limitku vynásobenú prvou nádhernou limitkou. Aby sme to urobili, rozložíme druhé mocniny x v čitateli a sínus v menovateli na identické faktory a aby sme dostali rovnaké koeficienty pre x a sínus, vydelíme x v čitateli 3 a hneď vynásobíme o 3. Dostaneme:

.

Príklad 4. Nájdite hranicu.

Riešenie. Opäť dostaneme neistotu „nula delená nulou“:

.

Môžeme získať pomer prvých dvoch pozoruhodných limitov. Čitateľ aj menovateľ delíme x. Potom, aby sa koeficienty sínusov a xes zhodovali, vynásobíme horné x 2 a hneď vydelíme 2 a dolné x vynásobíme 3 a hneď vydelíme 3. Dostaneme:

Príklad 5. Nájdite hranicu.

Riešenie. A opäť neistota „nula delená nulou“:

Z trigonometrie si pamätáme, že dotyčnica je pomer sínusu ku kosínusu a kosínus nuly sa rovná jednej. Vykonáme transformácie a získame:

.

Príklad 6. Nájdite hranicu.

Riešenie. Goniometrická funkcia pod znamienkom limity opäť naznačuje použitie prvej pozoruhodnej limity. Predstavujeme ho ako pomer sínusu ku kosínusu.