Príklady logaritmických výrazov a ich transformácií. Logaritmy

Inštrukcie

Napíšte daný logaritmický výraz. Ak výraz používa logaritmus 10, potom sa jeho zápis skráti a vyzerá takto: lg b je desiatkový logaritmus. Ak má logaritmus ako základ číslo e, napíšte výraz: ln b – prirodzený logaritmus. Rozumie sa, že výsledkom akéhokoľvek je mocnina, na ktorú sa musí základné číslo zvýšiť, aby sa získalo číslo b.

Pri hľadaní súčtu dvoch funkcií ich jednoducho musíte po jednej diferencovať a výsledky sčítať: (u+v)" = u"+v";

Pri hľadaní derivácie súčinu dvoch funkcií je potrebné vynásobiť deriváciu prvej funkcie druhou a pridať deriváciu druhej funkcie vynásobenú prvou funkciou: (u*v)" = u"*v +v"*u;

Aby sme našli deriváciu kvocientu dvoch funkcií, je potrebné od súčinu derivácie deliteľa vynásobeného funkciou deliteľa odpočítať súčin derivácie deliteľa vynásobeného funkciou deliteľa a rozdeliť to všetko pomocou funkcie deliteľa na druhú. (u/v)" = (u"*v-v"*u)/v^2;

Ak je daný komplexná funkcia, potom je potrebné vynásobiť deriváciu z vnútorná funkcia a derivát vonkajšieho. Nech y=u(v(x)), potom y"(x)=y"(u)*v"(x).

Pomocou vyššie získaných výsledkov môžete rozlíšiť takmer akúkoľvek funkciu. Pozrime sa teda na niekoľko príkladov:

y=x^4, y"=4*x^(4-1)=4*x^3;

y=2*x^3*(e^x-x^2+6), y"=2*(3*x^2*(e^x-x^2+6)+x^3*(e^x-2 *X));
Existujú aj problémy týkajúce sa výpočtu derivácie v bode. Nech je daná funkcia y=e^(x^2+6x+5), musíte nájsť hodnotu funkcie v bode x=1.
1) Nájdite deriváciu funkcie: y"=e^(x^2-6x+5)*(2*x +6).

2) Vypočítajte hodnotu funkcie v daný bod y"(1)=8*e^0=8

Video k téme

Užitočné rady

Naučte sa tabuľku základných derivácií. To výrazne ušetrí čas.

Zdroje:

• derivácia konštanty

Aký je teda rozdiel medzi iracionálnou a racionálnou rovnicou? Ak je neznáma premenná pod znamienkom druhej odmocniny, potom sa rovnica považuje za iracionálnu.

Inštrukcie

Hlavnou metódou riešenia takýchto rovníc je metóda konštrukcie oboch strán rovníc do štvorca. Avšak. je to prirodzené, prvá vec, ktorú musíte urobiť, je zbaviť sa znamienka. Táto metóda nie je technicky náročná, ale niekedy môže viesť k problémom. Napríklad rovnica je v(2x-5)=v(4x-7). Umocnením oboch strán získate 2x-5=4x-7. Riešenie takejto rovnice nie je ťažké; x=1. Ale číslo 1 nebude dané rovníc. prečo? Namiesto hodnoty x dosaďte do rovnice jedničku a pravá a ľavá strana budú obsahovať výrazy, ktoré nedávajú zmysel, tzn. Táto hodnota neplatí pre druhú odmocninu. Preto 1 je cudzí koreň, a preto daná rovnica nemá korene.

Iracionálna rovnica sa teda rieši metódou kvadratúry oboch jej strán. A po vyriešení rovnice je potrebné odrezať cudzie korene. Za týmto účelom nahraďte nájdené korene do pôvodnej rovnice.

Zvážte inú.
2х+vх-3=0
Samozrejme, že táto rovnica môže byť vyriešená pomocou rovnakej rovnice ako predchádzajúca. Presuňte zlúčeniny rovníc, ktoré nemajú druhú odmocninu, v pravá strana a potom použite metódu kvadratúry. vyriešiť výslednú racionálnu rovnicu a korene. Ale aj inú, elegantnejšiu. Zadajte novú premennú; vх=y. Podľa toho dostanete rovnicu v tvare 2y2+y-3=0. Teda bežné kvadratická rovnica. Nájdite jeho korene; y1 = 1 a y2 = -3/2. Ďalej vyriešte dve rovníc vх=1; vх=-3/2. Druhá rovnica nemá korene z prvej zistíme, že x=1. Nezabudnite skontrolovať korene.

Riešenie identít je celkom jednoduché. Na to je potrebné vykonať identické transformácie, kým sa nedosiahne cieľ. Pomocou jednoduchých aritmetických operácií bude teda úloha vyriešená.

Budete potrebovať

• - papier;
• - pero.

Inštrukcie

Najjednoduchšou z takýchto transformácií sú algebraické skrátené násobenia (napríklad druhá mocnina súčtu (rozdiel), rozdiel druhých mocnín, súčet (rozdiel), druhá mocnina súčtu (rozdiel)). Okrem toho existuje veľa goniometrických vzorcov, ktoré sú v podstate rovnakými identitami.

Druhá mocnina súčtu dvoch členov sa skutočne rovná štvorcu prvého plus dvojnásobku súčinu prvého a druhého a plus druhej mocniny druhého, teda (a+b)^2= (a+ b)(a+b)=a^2+ab +ba+b ^2=a^2+2ab+b^2.

Zjednodušte oboje

Všeobecné princípy riešenia

Zopakujte si z učebnice matematickej analýzy alebo vyššej matematiky, čo je to určitý integrál. Ako je známe, riešením určitého integrálu je funkcia, ktorej derivácia poskytne integrand. Táto funkcia sa nazýva primitívna. Autor: tento princíp a zostrojí hlavné integrály.
Určte podľa typu integrandu, ktorý z tabuľkových integrálov je v tomto prípade vhodný. Nie vždy sa to dá okamžite určiť. Často sa tabuľková forma stane viditeľnou až po niekoľkých transformáciách, aby sa integrand zjednodušil.

Variabilná náhradná metóda

Ak je integrand goniometrická funkcia, ktorej argument je polynóm, skúste použiť metódu zmeny premenných. Aby ste to dosiahli, nahraďte polynóm v argumente integrandu nejakou novou premennou. Na základe vzťahu medzi novými a starými premennými určte nové limity integrácie. Odlíšením tohto výrazu nájdite nový diferenciál v . Takže dostanete nový druh predchádzajúceho integrálu, blízkeho alebo dokonca zodpovedajúceho ktorémukoľvek tabuľkovému integrálu.

Riešenie integrálov druhého druhu

Ak je integrál integrálom druhého druhu, vektorovou formou integrandu, potom budete musieť použiť pravidlá na prechod z týchto integrálov na skalárne. Jedným z takýchto pravidiel je Ostrogradsky-Gaussov vzťah. Tento zákon nám umožňuje prejsť od rotorového toku určitej vektorovej funkcie k trojnému integrálu cez divergenciu daného vektorového poľa.

Substitúcia integračných limitov

Po nájdení primitívneho prvku je potrebné dosadiť hranice integrácie. Najprv dosaďte do výrazu pre primitívnu hodnotu hodnotu hornej hranice. Dostanete nejaké číslo. Potom od výsledného čísla odčítajte ďalšie číslo získané zo spodnej hranice do primitívnej funkcie. Ak je jednou z limitov integrácie nekonečno, potom pri jej dosadení do primitívnej funkcie je potrebné ísť na limitu a nájsť, k čomu výraz smeruje.
Ak je integrál dvojrozmerný alebo trojrozmerný, potom budete musieť geometricky reprezentovať hranice integrácie, aby ste pochopili, ako integrál vyhodnotiť. V skutočnosti v prípade, povedzme, trojrozmerného integrálu, limity integrácie môžu byť celé roviny, ktoré obmedzujú objem, ktorý sa integruje.

Zachovanie vášho súkromia je pre nás dôležité. Z tohto dôvodu sme vyvinuli Zásady ochrany osobných údajov, ktoré popisujú, ako používame a uchovávame vaše informácie. Prečítajte si naše postupy ochrany osobných údajov a ak máte nejaké otázky, dajte nám vedieť.

Zhromažďovanie a používanie osobných údajov

Osobné údaje sú údaje, ktoré možno použiť na identifikáciu alebo kontaktovanie konkrétnej osoby.

Keď nás budete kontaktovať, môžete byť kedykoľvek požiadaní o poskytnutie svojich osobných údajov.

Nižšie sú uvedené niektoré príklady typov osobných údajov, ktoré môžeme zhromažďovať, a ako môžeme tieto informácie použiť.

Aké osobné údaje zhromažďujeme:

• Keď odošlete žiadosť na stránke, môžeme zhromažďovať rôzne informácie vrátane vášho mena, telefónneho čísla, adresy Email atď.

Ako používame vaše osobné údaje:

• Osobné údaje, ktoré zhromažďujeme, nám umožňujú kontaktovať vás s jedinečnými ponukami, propagačnými akciami a inými udalosťami a pripravovanými udalosťami.
• Z času na čas môžeme použiť vaše osobné údaje na zasielanie dôležitých upozornení a komunikácie.
• Osobné údaje môžeme použiť aj na interné účely, ako je vykonávanie auditov, analýza údajov a rôzne výskumy, aby sme zlepšili služby, ktoré poskytujeme, a poskytli vám odporúčania týkajúce sa našich služieb.
• Ak sa zúčastníte žrebovania o ceny, súťaže alebo podobnej propagačnej akcie, môžeme použiť informácie, ktoré nám poskytnete, na správu takýchto programov.

Sprístupnenie informácií tretím stranám

Informácie, ktoré od vás dostaneme, nezverejňujeme tretím stranám.

Výnimky:

• V prípade potreby – v súlade so zákonom, súdnym konaním, v súdnom konaní a/alebo na základe verejných žiadostí alebo žiadostí vládnych orgánov na území Ruskej federácie – poskytnúť vaše osobné údaje. Môžeme tiež zverejniť informácie o vás, ak zistíme, že takéto zverejnenie je nevyhnutné alebo vhodné na účely bezpečnosti, presadzovania práva alebo na iné účely verejného významu.
• V prípade reorganizácie, zlúčenia alebo predaja môžeme osobné údaje, ktoré zhromažďujeme, preniesť na príslušnú nástupnícku tretiu stranu.

Ochrana osobných údajov

Prijímame opatrenia – vrátane administratívnych, technických a fyzických – na ochranu vašich osobných údajov pred stratou, krádežou a zneužitím, ako aj neoprávneným prístupom, zverejnením, zmenou a zničením.

Rešpektovanie vášho súkromia na úrovni spoločnosti

Aby sme zaistili bezpečnosť vašich osobných údajov, informujeme našich zamestnancov o štandardoch ochrany osobných údajov a bezpečnosti a prísne presadzujeme postupy ochrany osobných údajov.

EGOROVÁ VICTORIA VALERIEVNA

Učiteľ matematiky

najvyššie kvalifikačnej kategórii

TÉMA: „IDENTÁLNA TRANSFORMÁCIA

LOGARITMICKÉ VÝRAZY"

Vedomosti a zručnosti, ktoré by mali študenti po štúdiu ovládať túto lekciu:

poznať definíciu logaritmu čísla, základnú logaritmickú identitu, vlastnosti logaritmov;

byť schopný vykonávať transformácie výrazov obsahujúcich logaritmy a počítať logaritmy.

Literatúra:

1. Alimov Sh.A., Kolyagin Yu.M., Sidorov Yu.V. a iné Algebra a začiatky analýzy: učebnica pre ročníky 10-11 vo vzdelávacích inštitúciách. – M.: Vzdelávanie, 2001.

2. Kochagin V.V., Kochagina M.V., Intenzívny prípravný kurz na Jednotnú štátnu skúšku. – M.: Eksmo, 2009.

3. Merzlyak A.G., Polonsky V.B., Yakir M.S., Algebraický simulátor: Manuál pre školákov a uchádzačov. – M.: Ilexa, 2005.

4. Gusev V.A., Mordkovich A.G. Matematika: Referenčné materiály: Kniha pre študentov. – M.: Vzdelávanie, 2001.

Plán lekcie:

Počas tried:

1) Logaritmus je grécke slovo, ktoré pozostáva z 2 slov: „logos“ - pomer, „aritmos“ - číslo. To znamená, že logaritmus je číslo, ktoré meria pomer. V publikácii z roku 1614 sa uvádza, že Napier vynašiel logaritmy. Neskôr zostavil logaritmické tabuľky, ktoré sú nám dnes známe ako Bradisove tabuľky. Za menej ako storočie sa tabuľky rozšírili do celého sveta a stali sa nepostrádateľným výpočtovým nástrojom. Následne boli akoby zabudované do pohodlného zariadenia, ktoré značne urýchľovalo proces výpočtu - logaritmického pravítka, ktoré sa používalo až do sedemdesiatych rokov dvadsiateho storočia.

Príloha 1.

2) Logaritmus kladné číslob založené na a, a a je väčší ako nula a nie rovný jednej,je exponent, na ktorý sa musí číslo zvýšiťa získať číslob.

Táto rovnosť, vyjadrujúca definíciu logaritmu, sa nazývazákladná logaritmická identita .

C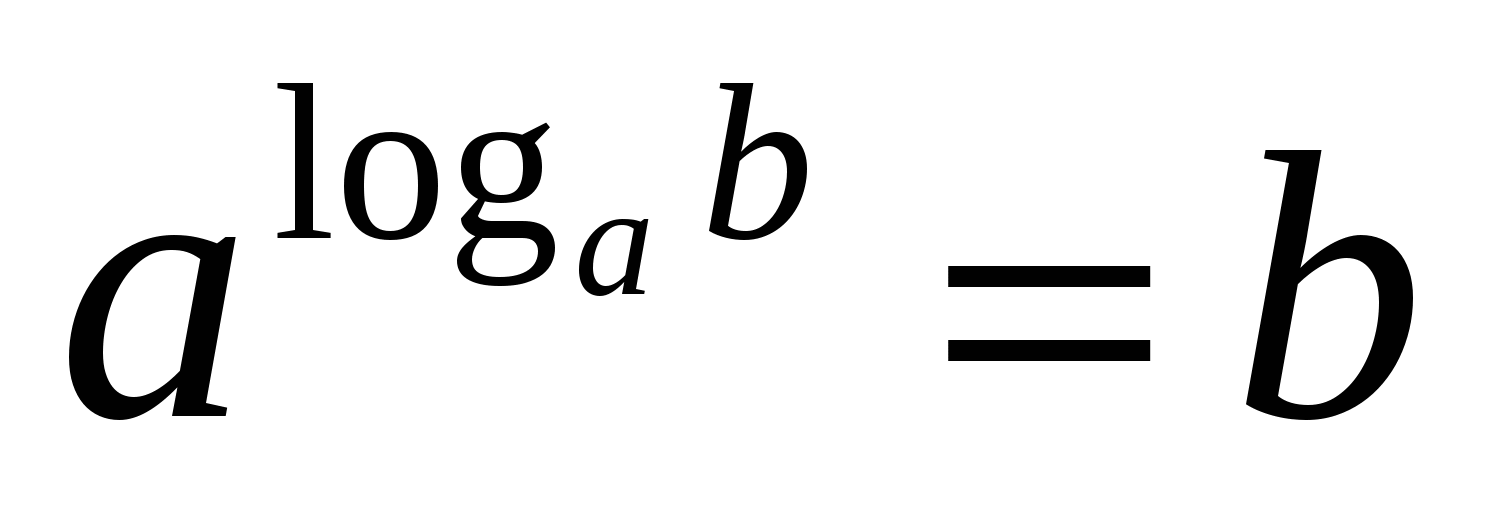

ALEBO 1

P

Základ mocniny a základ logaritmu je sedemnásť, čo znamená, že podľa základnej logaritmickej identity je hodnota výrazu tri.

Poďme na to ústne:

SCH
Jedľa

O spodná časť druhého sa rovná nule päť, čo znamená, že výraz sa rovná aritmetike odmocnina z piatich.

P

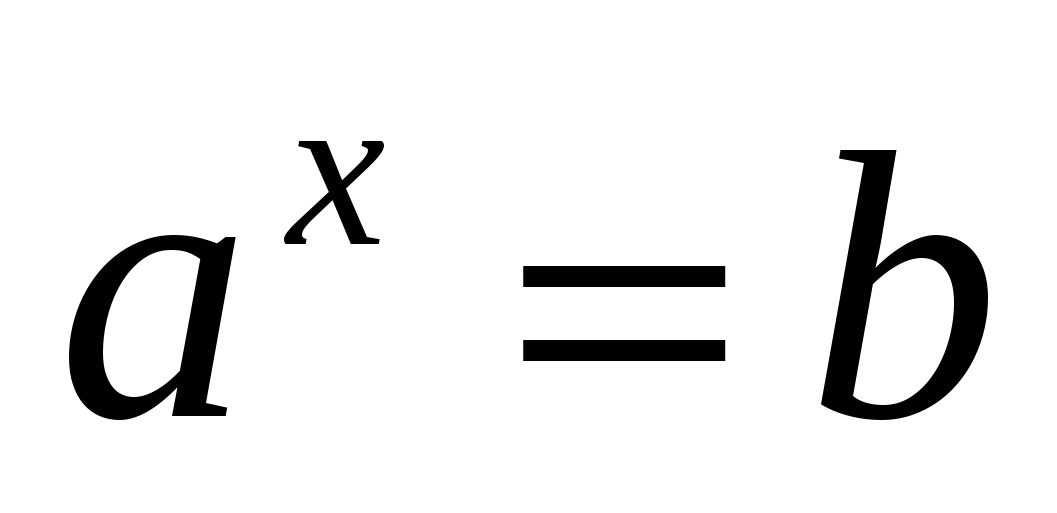Dodatok 2.

Rovnosť znamená to

Z definície logaritmu sa získajú nasledujúce dôležité rovnosti:

Napríklad:

P
Dodatok 3.

Prejdime k Zadania jednotnej štátnej skúšky:

Dodatok 4.

3
) Logaritmus základnej desiatky má špeciálny zápis a názovdesiatkový logaritmus .

L
základný kalaritmuse volalprirodzený logaritmus .

N
napríklad,

4) Nasledujúce vlastnosti vyplývajú z definície logaritmu. Všetky vlastnosti sú formulované a overené len pre kladné hodnoty premenné obsiahnuté pod logaritmickými znakmi.

Logaritmus súčinu dvoch kladných čísel k základu A rovná súčtu logaritmov týchto čísel s rovnakým základom.

TsOR 2

Napríklad,

Z
zadanie 1.

Úloha 2. Zjednodušte výraz

IN
Využime riešenie z predchádzajúceho príkladu. Nahradíme

Upozorňujeme, že logaritmus je na druhú, takže súčet musí byť na druhú. Pomocou vzorca pre druhú mocninu súčtu otvoríme zátvorky. Uveďme si podobné pojmy.

5) Logaritmus podielu sa rovná rozdielu medzi logaritmami dividendy a deliteľa.

C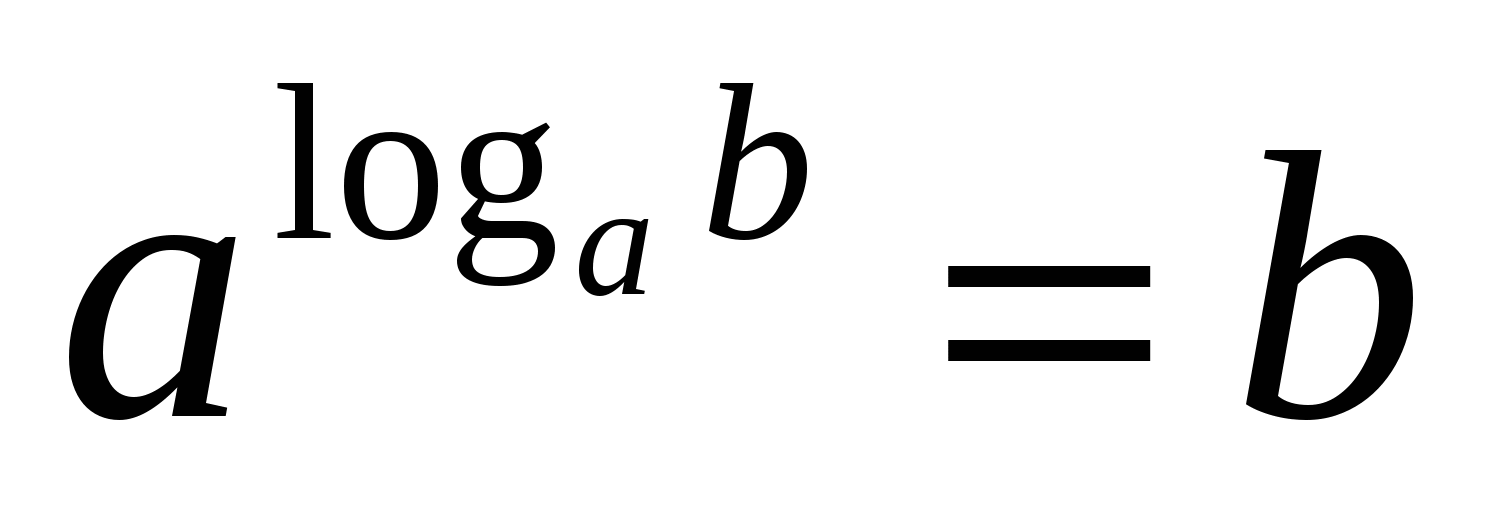

Dávajte pozor na základňu mocniny a základňu logaritmu - sú rovnaké.

ALEBO 3

R

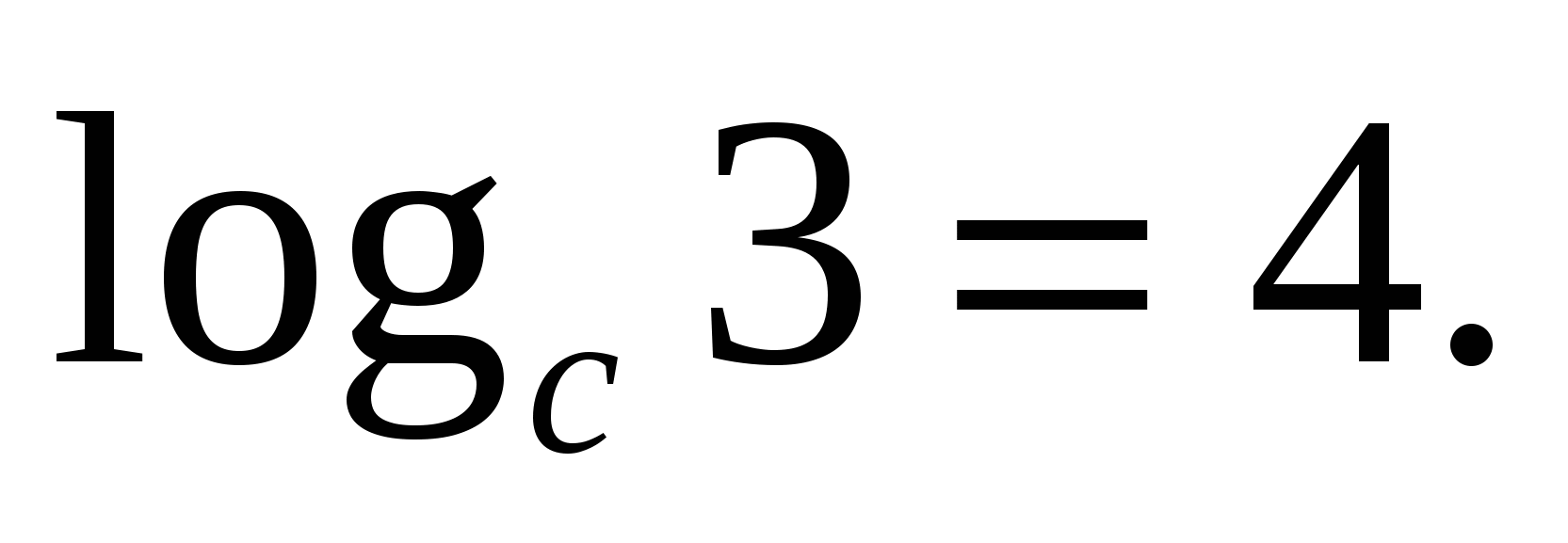Pozrime sa na použitie tohto vzorca pomocou príkladu:

Z
zadanie 1. Nájdite hodnotu výrazu if

Úloha 2. Nájdite hodnotu b podľa jeho logaritmu

6) Logaritmus výkonu k základniA , sa rovná súčinu exponentu a logaritmu s použitím rovnakého základu.

TsOR 4

Napríklad,

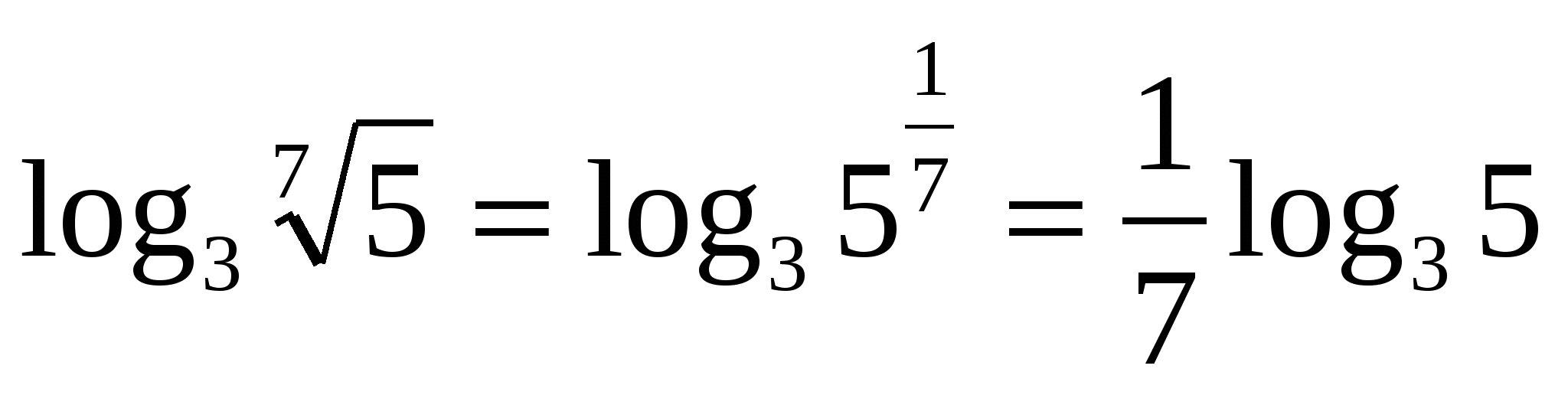
Z
zadanie 1. Vypočítajte, ak

Zjednodušme výraz

Vzorec

volal vzorec na prechod na nový základ.

Z

zadanie 1. Vyjadrite pomocou základného 2 logaritmu.

Úloha 2. Vypočítajte

TsOR 5

TsOR 6

Napríklad,

Z

zadanie 1. Vypočítajte

Z
úloha 2. Vypočítajte

9) Logaritmické transformácie je možné spustiť iba v prípadoch, keď ak si pamätáte všetky vlastnosti logaritmov. Po ich zopakovaní zvážime úlohy na transformáciu logaritmických výrazov z druhej strany.

Na prevod súčtu alebo rozdielu logaritmických výrazov niekedy stačí použiť definíciu logaritmu a najčastejšie vlastnosti logaritmu súčinu alebo kvocientu.

Z
zadanie 1. Vypočítajte

Poďme to vyriešiť dvoma spôsobmi.

1 spôsob pomocou definície logaritmu:

Metóda 2, založená na vlastnosť logaritmu kvocientu:

Úloha 2. Nájdite význam výrazu

Najprv aplikujme vzorec logaritmus súčinu, potom definícia logaritmu.

Základná logaritmická identita sa používa pri konverzii výrazov obsahujúcich logaritmus ako exponent. Myšlienkou takýchto operácií je získať rovnaké základy mocnin a základov logaritmu.

Niekedy je potrebné výraz transformovať podľa vlastností logaritmu a podľa vlastností stupňa môžete jednoducho prejsť z jednej základne na druhú pomocou prechodového vzorca. V ostatných prípadoch by sa mali použiť viaceré vlastnosti.

Z
úloha 3. Vypočítajte

Z
zadanie 4. Nájdite význam výrazu

Úloha 5. Nájdite význam výrazu

Z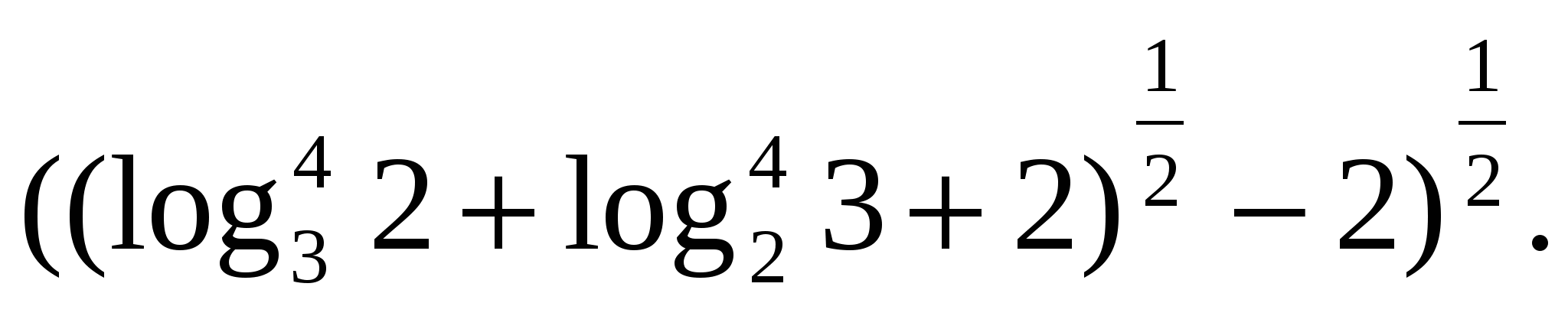
úloha 6. Vyjadrite to ako rozdiel logaritmov

N
Najväčší problém je pri prevode logaritmických výrazov pod radikál. V procese transformácií je potrebné zvážiť moduly logaritmických výrazov, na vyriešenie ktorých je potrebné porovnávať iracionálne čísla alebo racionálne a iracionálne číslo. Budeme konať dôsledne. Pozrime sa na výraz pod vnútorným radikálom.

Dosadíme to do pôvodného výrazu.

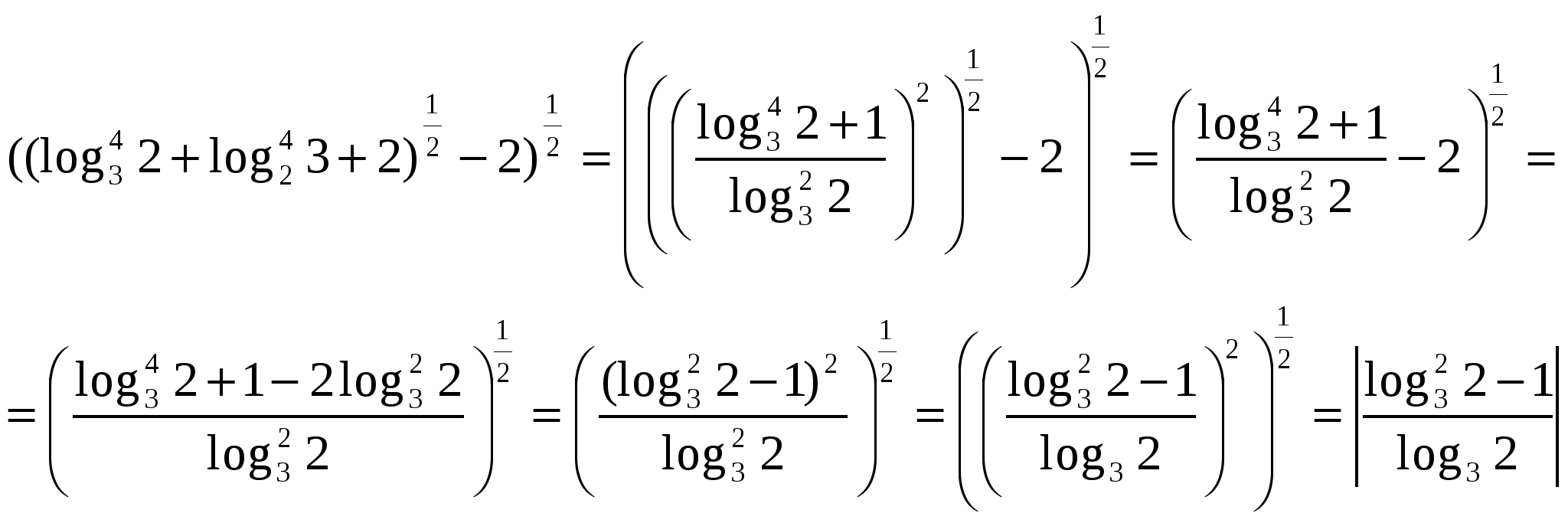Treba poznamenať, že s transformáciou logaritmických výrazov sa môžeme stretnúť aj pri riešení rovníc a nerovníc alebo pri štúdiu funkcií, preto môžu byť v úlohách skupín B a C prítomné v implicitnej forme.

10) Zhrnutie otázok:

Volá sa logaritmus so základom 10

základný logaritmus

hlavný logaritmus

prirodzený logaritmus

desiatkový logaritmus

2) Aké hodnoty môže nadobudnúť?X vo výraze

Hodnota nie je definovaná

5) Uveďte pomer, ktorý platí pre všetkýchX ≠ 0 .

6) Uveďte správny pomer pre vzorec pre prechod na nový základ.

7) Zadajte správnu rovnosť pre

11) Kontrolné testovanie.

Ako viete, pri násobení výrazov mocninami sa ich exponenty vždy sčítajú (a b *a c = a b+c). Tento matematický zákon odvodil Archimedes a neskôr, v 8. storočí, vytvoril matematik Virasen tabuľku celočíselných exponentov. Boli to oni, ktorí slúžili na ďalšie objavovanie logaritmov. Príklady využitia tejto funkcie nájdete takmer všade tam, kde si potrebujete zjednodušiť ťažkopádne násobenie jednoduchým sčítaním. Ak strávite 10 minút čítaním tohto článku, vysvetlíme vám, čo sú to logaritmy a ako s nimi pracovať. Jednoduchým a prístupným jazykom.

Definícia v matematike

Logaritmus je vyjadrením nasledujúceho tvaru: log a b=c, teda logaritmus ľubovoľného nezáporného čísla (teda akéhokoľvek kladného) „b“ k základu „a“ sa považuje za mocninu „c“. “, na ktorú musí byť základ „a“ zvýšený, aby sa v konečnom dôsledku získala hodnota „b“. Analyzujme logaritmus na príkladoch, povedzme, že existuje výraz log 2 8. Ako nájsť odpoveď? Je to veľmi jednoduché, musíte nájsť výkon tak, aby od 2 po požadovaný výkon dostal 8. Po vykonaní niekoľkých výpočtov v hlave dostaneme číslo 3! A to je pravda, pretože 2 ku 3 dáva odpoveď ako 8.

Typy logaritmov

Pre mnohých žiakov a študentov sa táto téma zdá komplikovaná a nepochopiteľná, ale v skutočnosti logaritmy nie sú také strašidelné, hlavnou vecou je pochopiť ich všeobecný význam a zapamätať si ich vlastnosti a niektoré pravidlá. Sú tam tri jednotlivé druhy logaritmické výrazy:

1. Prirodzený logaritmus ln a, kde základom je Eulerovo číslo (e = 2,7).
2. Desatinné a, kde základ je 10.
3. Logaritmus ľubovoľného čísla b na základ a>1.

Každá z nich je riešená štandardným spôsobom, vrátane zjednodušenia, redukcie a následnej redukcie na jeden logaritmus pomocou logaritmických viet. Aby ste získali správne hodnoty logaritmov, mali by ste si pamätať ich vlastnosti a postupnosť akcií pri ich riešení.

Pravidlá a určité obmedzenia

V matematike existuje niekoľko pravidiel-obmedzení, ktoré sú akceptované ako axióma, to znamená, že nie sú predmetom diskusie a sú pravdivé. Napríklad nie je možné deliť čísla nulou a tiež nie je možné z nich extrahovať párny koreň záporné čísla. Logaritmy majú tiež svoje pravidlá, podľa ktorých sa ľahko naučíte pracovať aj s dlhými a objemnými logaritmickými výrazmi:

• Základ „a“ musí byť vždy väčší ako nula a nie rovný 1, inak výraz stratí svoj význam, pretože „1“ a „0“ sa v akomkoľvek stupni vždy rovnajú svojim hodnotám;
• ak a > 0, potom a b > 0, ukáže sa, že „c“ musí byť tiež väčšie ako nula.

Ako vyriešiť logaritmy?

Úlohou je napríklad nájsť odpoveď na rovnicu 10 x = 100. Je to veľmi jednoduché, treba zvoliť mocninu zvýšením čísla desať, na ktoré sa dostaneme 100. To je samozrejme 10 2 = 100.

Teraz si predstavme tento výraz v logaritmickej forme. Dostaneme log 10 100 = 2. Pri riešení logaritmov sa všetky akcie prakticky zbiehajú, aby našli mocninu, do ktorej je potrebné zadať základ logaritmu, aby sme získali dané číslo.

Ak chcete presne určiť hodnotu neznámeho stupňa, musíte sa naučiť pracovať s tabuľkou stupňov. Vyzerá to takto:

Ako vidíte, niektoré exponenty sa dajú uhádnuť intuitívne, ak máte technické myslenie a znalosti násobilky. Pre väčšie hodnoty však budete potrebovať tabuľku výkonu. Využiť ho môžu aj tí, ktorí o zložitých matematických témach nevedia vôbec nič. Ľavý stĺpec obsahuje čísla (základ a), horný riadok čísel je hodnota mocniny c, na ktorú je číslo a umocnené. Na priesečníku bunky obsahujú číselné hodnoty, ktoré sú odpoveďou (a c = b). Zoberme si napríklad úplne prvú bunku s číslom 10 a odmocnime ju, dostaneme hodnotu 100, ktorá je naznačená na priesečníku našich dvoch buniek. Všetko je také jednoduché a ľahké, že to pochopí aj ten najpravdivejší humanista!

Rovnice a nerovnice

Ukazuje sa, že za určitých podmienok je exponentom logaritmus. Preto akékoľvek matematické numerické výrazy možno zapísať ako logaritmickú rovnosť. Napríklad 3 4 = 81 možno zapísať ako základný 3 logaritmus 81 rovný štyrom (log 3 81 = 4). Pre negatívne sily pravidlá sú rovnaké: 2 -5 = 1/32 zapíšeme to ako logaritmus, dostaneme log 2 (1/32) = -5. Jednou z najfascinujúcejších častí matematiky je téma „logaritmov“. Na príklady a riešenia rovníc sa pozrieme nižšie, hneď po preštudovaní ich vlastností. Teraz sa pozrime, ako vyzerajú nerovnosti a ako ich odlíšiť od rovníc.

Je daný výraz v nasledujúcom tvare: log 2 (x-1) > 3 - je logaritmická nerovnosť, pretože neznáma hodnota "x" je pod znamienkom logaritmu. A tiež vo výraze sa porovnávajú dve veličiny: logaritmus požadovaného čísla so základom dva je väčší ako číslo tri.

Najdôležitejší rozdiel medzi logaritmickými rovnicami a nerovnicami je v tom, že rovnice s logaritmami (príklad - logaritmus 2 x = √9) zahŕňajú jednu alebo viac konkrétnych číselných hodnôt v odpovedi, zatiaľ čo pri riešení nerovností sú definované ako oblasť prijateľné hodnoty a body prerušenia tejto funkcie. V dôsledku toho odpoveď nie je jednoduchá množina jednotlivých čísel ako v odpovedi na rovnicu, ale súvislý rad alebo množina čísel.

Základné vety o logaritmoch

Pri riešení primitívnych úloh hľadania hodnôt logaritmu nemusia byť jeho vlastnosti známe. Pokiaľ však ide o logaritmické rovnice alebo nerovnice, v prvom rade je potrebné jasne pochopiť a prakticky aplikovať všetky základné vlastnosti logaritmov. Na príklady rovníc sa pozrieme neskôr, pozrime sa na každú vlastnosť podrobnejšie.

1. Hlavná identita vyzerá takto: a logaB =B. Platí len vtedy, keď a je väčšie ako 0, nerovná sa jednej a B je väčšie ako nula.
2. Logaritmus súčinu môže byť vyjadrený v nasledujúcom vzorci: log d (s 1 * s 2) = log d s 1 + log d s 2. V tomto prípade je povinná podmienka: d, s 1 a s 2 > 0; a≠1. Tento logaritmický vzorec môžete dokázať príkladmi a riešením. Nech log a s 1 = f 1 a log a s 2 = f 2, potom a f1 = s 1, a f2 = s 2. Dostaneme, že s 1 * s 2 = a f1 *a f2 = a f1+f2 (vlastnosti stupne ), a potom podľa definície: log a (s 1 * s 2) = f 1 + f 2 = log a s1 + log a s 2, čo bolo potrebné dokázať.
3. Logaritmus kvocientu vyzerá takto: log a (s 1/ s 2) = log a s 1 - log a s 2.
4. Veta vo forme vzorca má tento tvar: log a q b n = n/q log a b.

Tento vzorec sa nazýva „vlastnosť stupňa logaritmu“. Pripomína vlastnosti bežných stupňov a nie je to prekvapujúce, pretože celá matematika je založená na prirodzených postulátoch. Pozrime sa na dôkaz.

Nech log a b = t, ukáže sa a t =b. Ak obe časti zdvihneme na mocninu m: a tn = b n ;

ale keďže a tn = (a q) nt/q = b n, preto log a q b n = (n*t)/t, potom log a q b n = n/q log a b. Veta bola dokázaná.

Príklady problémov a nerovností

Najbežnejšími typmi problémov na logaritmoch sú príklady rovníc a nerovníc. Nachádzajú sa takmer vo všetkých problémových knihách a sú tiež povinnou súčasťou skúšok z matematiky. Ak chcete vstúpiť na univerzitu alebo zložiť prijímacie skúšky z matematiky, musíte vedieť, ako správne riešiť takéto úlohy.

Bohužiaľ neexistuje jednotný plán alebo schéma na riešenie a určenie neznámej hodnoty logaritmu, dá sa však použiť na každú matematickú nerovnosť alebo logaritmickú rovnicu. určité pravidlá. V prvom rade by ste si mali zistiť, či sa výraz dá zjednodušiť alebo naviesť celkový vzhľad. Dlhé logaritmické výrazy môžete zjednodušiť, ak správne použijete ich vlastnosti. Poďme sa s nimi rýchlo zoznámiť.

Pri riešení logaritmických rovníc musíme určiť, aký typ logaritmu máme: príklad výrazu môže obsahovať prirodzený logaritmus alebo desiatkový.

Tu sú príklady ln100, ln1026. Ich riešenie sa scvrkáva na skutočnosť, že potrebujú určiť výkon, s ktorým bude základ 10 rovný 100 a 1026. Ak chcete vyriešiť prirodzené logaritmy, musíte použiť logaritmické identity alebo ich vlastnosti. Pozrime sa na príklady riešenia logaritmických problémov rôznych typov.

Ako používať logaritmické vzorce: s príkladmi a riešeniami

Pozrime sa teda na príklady použitia základných teorémov o logaritmoch.

1. Vlastnosť logaritmu súčinu môže byť použitá v úlohách, kde je potrebné expandovať veľký významčísla b do jednoduchších faktorov. Napríklad log 2 4 + log 2 128 = log 2 (4*128) = log 2 512. Odpoveď je 9.
2. log 4 8 = log 2 2 2 3 = 3/2 log 2 2 = 1,5 - ako vidíte, pomocou štvrtej vlastnosti logaritmu sa nám podarilo vyriešiť zdanlivo zložitý a neriešiteľný výraz. Stačí vypočítať základ a potom odobrať hodnoty exponentov zo znamienka logaritmu.

Úlohy z jednotnej štátnej skúšky

Logaritmy sa často vyskytujú pri prijímacích skúškach, najmä veľa logaritmických problémov pri Jednotnej štátnej skúške (štátna skúška pre všetkých absolventov škôl). Tieto úlohy sa zvyčajne nachádzajú nielen v časti A (najjednoduchšia testovacia časť skúšky), ale aj v časti C (najkomplexnejšie a najobsiahlejšie úlohy). Skúška vyžaduje presnú a dokonalú znalosť témy „Prirodzené logaritmy“.

Príklady a riešenia problémov sú prevzaté z oficiálnych Možnosti jednotnej štátnej skúšky. Pozrime sa, ako sa takéto úlohy riešia.

Dané log 2 (2x-1) = 4. Riešenie:
prepíšme výraz, trochu ho zjednodušíme log 2 (2x-1) = 2 2, podľa definície logaritmu dostaneme, že 2x-1 = 2 4, teda 2x = 17; x = 8,5.

• Najlepšie je zredukovať všetky logaritmy na rovnaký základ, aby riešenie nebolo ťažkopádne a mätúce.
• Všetky výrazy pod logaritmickým znamienkom sú označené ako kladné, preto keď exponent výrazu, ktorý je pod logaritmickým znamienkom a ako jeho základ sa vyberie ako násobiteľ, výraz zostávajúci pod logaritmom musí byť kladný.

Úlohy, ktorých riešením je prevod logaritmických výrazov, sú na Jednotnej štátnej skúške celkom bežné.

Aby ste sa s nimi úspešne vyrovnali s minimálnym časom, musíte okrem základných logaritmických identít poznať a správne používať aj ďalšie vzorce.

Toto je: a log a b = b, kde a, b > 0, a ≠ 1 (Vyplýva to priamo z definície logaritmu).

log a b = log c b / log c a alebo log a b = 1/log b a
kde a, b, c > 0; a, c ≠ 1.

log a m b n = (m/n) log |a| |b|
kde a, b > 0, a ≠ 1, m, n Є R, n ≠ 0.

a log c b = b log c a
kde a, b, c > 0 a a, b, c ≠ 1

Aby sme ukázali platnosť štvrtej rovnosti, zoberme logaritmus ľavej a pravej strany na základ a. Dostaneme log a (a log s b) = log a (b log s a) alebo log s b = log s a · log a b; log c b = log c a · (log c b / log c a); log s b = log s b.

Dokázali sme rovnosť logaritmov, čo znamená, že aj výrazy pod logaritmami sú rovnaké. Formula 4 sa osvedčila.

Príklad 1

Vypočítajte 81 log 27 5 log 5 4 .

Riešenie.

81 = 3 4 , 27 = 3 3 .

log 27 5 = 1/3 log 3 5, log 5 4 = log 3 4 / log 3 5.

log 27 5 log 5 4 = 1/3 log 3 5 (log 3 4 / log 3 5) = 1/3 log 3 4.

Potom 81 log 27 5 log 5 4 = (3 4) 1/3 log 3 4 = (3 log 3 4) 4/3 = (4) 4/3 = 4 3 √4.

Nasledujúcu úlohu môžete splniť sami.

Vypočítajte (8 log 2 3 + 3 1/ log 2 3) - log 0,2 5.

Ako pomôcka, 0,2 = 1/5 = 5-1; log 0,25 = -1.

odpoveď: 5.

Príklad 2

Vypočítať (√11) log √3 9- log 121 81 .

Riešenie.

Zmeňme výrazy: 9 = 3 2, √3 = 3 1/2, log √3 9 = 4,

121 = 11 2, 81 = 3 4, log 121 81 = 2 log 11 3 (bol použitý vzorec 3).

Potom (√11) log √3 9- log 121 81 = (11 1/2) 4-2 log 11 3 = (11) 2- log 11 3 = 11 2 / (11) log 11 3 = 11 2 / ( 11 log 11 3) = 121/3.

Príklad 3

Vypočítajte log 2 24 / log 96 2 - log 2 192 / log 12 2.

Riešenie.

Logaritmy obsiahnuté v príklade nahradíme logaritmami so základom 2.

log 96 2 = 1/log 2 96 = 1/log 2 (2 5 3) = 1/(log 2 2 5 + log 2 3) = 1/(5 + log 2 3);

log 2 192 = log 2 (2 6 3) = (log 2 2 6 + log 2 3) = (6 + log 2 3);

log 2 24 = log 2 (2 3 3) = (log 2 2 3 + log 2 3) = (3 + log 2 3);

log 12 2 = 1/log 2 12 = 1/log 2 (2 2 3) = 1/(log 2 2 2 + log 2 3) = 1/(2 + log 2 3).

Potom log 2 24 / log 96 2 – log 2 192 / log 12 2 = (3 + log 2 3) / (1/(5 + log 2 3)) – ((6 + log 2 3) / (1/( 2 + log 2 3)) =

= (3 + log 2 3) · (5 + log 2 3) – (6 + log 2 3)(2 + log 2 3).

Po otvorení zátvoriek a prinesení podobných pojmov dostaneme číslo 3. (Pri zjednodušení výrazu môžeme log 2 3 označiť n a výraz zjednodušiť

(3 + n) · (5 + n) – (6 + n) (2 + n)).

odpoveď: 3.

Nasledujúcu úlohu môžete dokončiť sami:

Vypočítať (log 3 4 + log 4 3 + 2) log 3 16 log 2 144 3.

Tu je potrebné urobiť prechod na logaritmy so základom 3 a faktorizáciu veľkých čísel na prvočiniteľa.

Odpoveď: 1/2

Príklad 4.

Dané tri čísla A = 1/(log 3 0,5), B = 1/(log 0,5 3), C = log 0,5 12 – log 0,5 3. Zoraď ich vzostupne.

Riešenie.

Transformujme čísla A = 1/(log 3 0,5) = log 0,5 3; C = log 0,5 12 – log 0,5 3 = log 0,5 12/3 = log 0,5 4 = -2.

Poďme si ich porovnať

log 0,5 3 > log 0,5 4 = -2 a log 0,5 3< -1 = log 0,5 2, так как функция у = log 0,5 х – убывающая.

Alebo 2< log 0,5 3 < -1. Тогда -1 < 1/(log 0,5 3) < -1/2.

Odpoveď. Preto je poradie umiestňovania čísel: C; A; IN.

Príklad 5.

Koľko celých čísel je v intervale (log 3 1 / 16 ; log 2 6 48).

Riešenie.

Určme, medzi ktorými mocninami čísla 3 sa nachádza číslo 1/16. Dostaneme 1/27< 1 / 16 < 1 / 9 .

Pretože funkcia y = log 3 x je rastúca, potom log 3 (1 / 27)< log 3 (1 / 16) < log 3 (1 / 9); -3 < log 3 (1 / 16) < -2.

log 648 = log 6 (36 4 / 3) = log 6 36 + log 6 (4 / 3) = 2 + log 6 (4 / 3). Porovnajme log 6 (4/3) a 1/5. A preto porovnávame čísla 4/3 a 6 1/5. Zvýšme obe čísla na 5. mocninu. Dostaneme (4/3) 5 = 1024 / 243 = 4 52 / 243< 6. Следовательно,

denník 6 (4/3)< 1 / 5 . 2 < log 6 48 < 2 1 / 5 . Числа, входящие в двойное неравенство, положительные. Их можно возводить в квадрат. Знаки неравенства при этом не изменятся. Тогда 4 < log 6 2 48 < 4 21 / 25.

Preto interval (log 3 1/16 ; log 6 48) zahŕňa interval [-2; 4] a naň sú umiestnené celé čísla -2; -1; 0; 1; 2; 3; 4.

Odpoveď: 7 celých čísel.

Príklad 6.

Vypočítajte 3 lglg 2/ lg 3 - lg20.

Riešenie.

3 lg lg 2/ lg 3 = (3 1/ lg3) lg lg 2 = (3 l® g 3 10) lg lg 2 = 10 lg lg 2 = lg2.

Potom 3 lglg2/lg3 - lg 20 = lg 2 – lg 20 = lg 0,1 = -1.

odpoveď: -1.

Príklad 7.

Je známe, že log 2 (√3 + 1) + log 2 (√6 – 2) = A. Nájdite log 2 (√3 –1) + log 2 (√6 + 2).

Riešenie.

Čísla (√3 + 1) a (√3 – 1); (√6 – 2) a (√6 + 2) sú konjugované.

Urobme nasledujúcu transformáciu výrazov

√3 – 1 = (√3 – 1) · (√3 + 1)) / (√3 + 1) = 2/(√3 + 1);

√6 + 2 = (√6 + 2) · (√6 – 2)) / (√6 – 2) = 2/(√6 – 2).

Potom log 2 (√3 – 1) + log 2 (√6 + 2) = log 2 (2/(√3 + 1)) + log 2 (2/(√6 – 2)) =

Log 2 2 – log 2 (√3 + 1) + log 2 2 – log 2 (√6 – 2) = 1 – log 2 (√3 + 1) + 1 – log 2 (√6 – 2) =

2 – log 2 (√3 + 1) – log 2 (√6 – 2) = 2 – A.

Odpoveď: 2 - A.

Príklad 8.

Zjednodušte a nájdite približnú hodnotu výrazu (log 3 2 log 4 3 log 5 4 log 6 5 ... log 10 9.

Riešenie.

Zredukujme všetky logaritmy na spoločný základ 10.

(log 3 2 log 4 3 log 5 4 log 6 5 ... log 10 9 = (lg 2 / lg 3) (lg 3 / lg 4) (lg 4 / lg 5) (lg 5 / lg 6) · … · (lg 8 / lg 9) · lg 9 = lg 2 ≈ 0,3010 (Približnú hodnotu lg 2 možno zistiť pomocou tabuľky, logaritmu alebo kalkulačky).

Odpoveď: 0,3010.

Príklad 9.

Vypočítajte log a 2 b 3 √ (a 11 b -3), ak log √ a b 3 = 1. (V tomto príklade je a 2 b 3 základom logaritmu).

Riešenie.

Ak log √ a b 3 = 1, potom 3/(0,5 log a b = 1. A log a b = 1/6.

Potom log a 2 b 3√ (a 11 b -3) = 1/2 log a 2 b 3 (a 11 b -3) = log a (a 11 b -3) / (2log a (a 2 b 3) ) = (log a a 11 + log a b -3) / (2(log a a 2 + log a b 3)) = (11 – 3log a b) / (2(2 + 3log a b)) Vzhľadom na to, že log a b = 1/ 6 dostaneme (11 – 3 1 / 6) / (2(2 + 3 1 / 6)) = 10,5/5 = 2,1.

Odpoveď: 2.1.

Nasledujúcu úlohu môžete dokončiť sami:

Vypočítajte log √3 6 √2,1, ak log 0,7 27 = a.

Odpoveď: (3 + a) / (3a).

Príklad 10.

Vypočítajte 6,5 4/ log 3 169 · 3 1/ log 4 13 + log125.

Riešenie.

6,5 4/ log 3 169 · 3 1/ log 4 13 + log 125 = (13/2) 4/2 log 3 13 · 3 2/ log 2 13 + 2 log 5 5 3 = (13/2) 2 log 13 3 3 2 log 13 2 + 6 = (13 log 13 3 / 2 log 13 3) 2 (3 log 13 2) 2 + 6 = (3/2 log 13 3) 2 (3 log 13 2) 2 + 6 = ( 3 2 /(2 log 13 3) 2) · (2 ​​log 13 3) 2 + 6.

(2 log 13 3 = 3 log 13 2 (vzorec 4))

Dostaneme 9 + 6 = 15.

odpoveď: 15.

Stále máte otázky? Neviete, ako nájsť hodnotu logaritmického výrazu?
Ak chcete získať pomoc od tútora, zaregistrujte sa.
Prvá lekcia je zadarmo!

webová stránka, pri kopírovaní celého materiálu alebo jeho časti sa vyžaduje odkaz na pôvodný zdroj.