Syntéza rekurzívne filtre založené na analógovom prototype

Pri syntéze štandardných frekvenčne selektívnych filtrov je vhodné použiť dobre vyvinutý prístroj na výpočet analógových filtrov. Väčšina široké využitie dostali nasledujúce metódy:

1. Invariantná metóda impulznej odozvy (štandardná transformačná metóda).

2. Metóda bilineárnej transformácie.

3. Metóda nahradenia derivátov konečnými rozdielmi.

4.2.1. Impulzná metóda invariantnosti (štandardná - transformačná metóda)

Invariantnosť impulznej odozvy sa chápe ako rovnosť vzoriek impulznej odozvy digitálneho filtra k hodnotám impulznej odozvy analógového prototypu, meraných s periódou vzorkovania.

Na implementáciu metódy, ktorú potrebujete:

Nájdite impulznú odozvu prototypu;

Získajte impulznú odozvu digitálneho filtra odberom vzoriek s periódou zohľadňujúcou faktor mierky:

; (4.1)

Nájdite funkciu prenosu filtra tak, že vezmete - transformáciu z :

. (4.2)

Obrázok 3.1 – vzorkovanie impulznej odozvy analógového prototypu

Predpokladajme, že prenosová funkcia analógového prototypu je napísaná ako súčet jednoduchých zlomkov:

. (4.3)

V tomto prípade v súlade s inverznou Laplaceovou transformáciou má impulzová odozva analógového prototypu nasledujúcu formu:

. (4.4)

Po vzorkovaní získame požadovanú impulznú odozvu digitálneho filtra:

Prenosová funkcia syntetizovaného digitálneho filtra v dôsledku aplikácie transformácie má nasledujúci tvar:

Výsledná prenosová funkcia zodpovedá paralelnej štruktúre digitálneho filtra. Bloková schéma jedného článku syntetizovaného digitálneho filtra s prenosovou charakteristikou vyzerá takto: Obrázok 3.2.

Obrázok 3.2 – bloková schéma jednej sekcie digitálneho filtra

Postup syntézy digitálnych filtrov pomocou metódy invariantnej impulznej odozvy teda obsahuje nasledujúce kroky:

1. Nastavte požiadavky na digitálny filter.

3. Rozdeľte na jednoduché zlomky.

4. Napíšte prenosovú funkciu digitálneho filtra na základe vzťahov (4.3) a (4.6).

Frekvenčná odozva výsledného filtra súvisí s frekvenčnou odozvou analógového prototypu rovnakým spôsobom, ako spektrum vzorkovaného signálu súvisí so spektrom analógového signálu: periodické opakovanie. Preto získať dobré výsledky Pre túto metódu musí byť zisk analógového prototypu zanedbateľný pri frekvenciách nad Nyquistovou frekvenciou. Preto je metóda vhodná na vytváranie dolnopriepustných filtrov a PF, ale nie je použiteľná na vývoj hornopriepustných filtrov a RF filtrov.

Príklad použitia metódy invariantnosti impulznej odozvy

Nech má prenosová funkcia analógového prototypu nasledujúci tvar:

.

V súlade s výrazom (4.3) je teda možné zapísať nasledujúce parametre analógového prototypu:

,

.

V súlade s výrazom (4.6) získame nasledujúci výraz pre prenosovú funkciu požadovaného digitálneho filtra:

.

Získame rovnicu digitálneho filtrovania. Za týmto účelom napíšeme prenosovú funkciu digitálneho filtra v tvare:

,

Kde ,

.

V dôsledku série matematických transformácií posledného výrazu môžeme získať:

,

Po prechode od obrázkov z-transformácie k originálom získame rovnicu digitálneho filtrovania:

4.2.2. Metóda bilineárnej transformácie

Laplaceova transformácia a - transformácia spolu súvisia vzťahom:

. (4.7)

Výraz (4.7) nemožno priamo použiť na výpočet digitálneho filtra so známou prenosovou charakteristikou analógového prototypu, pretože inverzný vzťah je transcendentálny:

. (4.8)

Tento problém je prekonaný použitím rozšírenia série:

.

Pomocou prvého členu rozšírenia môžeme získať:

. (4.9)

Táto transformácia je zlomkovou racionálnou funkciou argumentu prvého rádu a nazýva sa bilineárne z – transformácia.

Prenosová funkcia digitálneho filtra sa získa z prenosovej funkcie analógového prototypu pomocou nasledujúcej substitúcie:

. (4.10)

Uvažujme o vlastnostiach bilineárnej transformácie. Za to dostaneme:

. (4.11)

Bilineárna transformácia teda vedie k výraznej deformácii frekvenčnej odozvy prototypového analógu pri jeho prevode do digitálnej podoby v porovnaní s pôvodným pomerom. . Vzťah medzi frekvenciami frekvenčnej odozvy prototypu a frekvenciami digitálneho filtra sa určuje zo vzťahu:

.

Konečný vzťah medzi frekvenciou analógového prototypu a frekvenciou digitálneho filtra je nasledovný:

. (4.12)

V súlade s posledným výrazom je celá os osi nekonečnej frekvenčnej odozvy analógového prototypu úplne umiestnená v Nyquistovom intervale na digitálnej frekvenčnej osi od 0 do : Obrázok 3.3. V dôsledku toho je úplne eliminovaný efekt superpozície kópií frekvenčných charakteristík, ktorý je vlastný metóde invariantnosti impulznej odozvy. V nízkofrekvenčnom rozsahu sú frekvenčné charakteristiky analógových a digitálnych filtrov rovnaké:

. (4.13)

Obrázok 3.3 – transformácia frekvenčnej osi pri bilineárnej transformácii

Účinok deformácie frekvenčnej odozvy sa ľahko berie do úvahy pre frekvenčne selektívne filtre charakterizované hranicami priepustného pásma s použitím posledného výrazu frekvenčnej väzby.

Postup výpočtu filtra je nasledujúci:

1) Frekvenčná charakteristika vypočítaného filtra je nastavená na frekvenčnej škále a charakteristické body frekvenčnej charakteristiky sú vyznačené na tej istej stupnici.

2) Použitie transformačnej funkcie rovnaké charakteristické body sú určené na frekvenčnej škále pre analógový prototyp a je zostavený výraz pre jeho prenosovú funkciu.

3) Pomocou metódy bilineárnej transformácie sa prenosová funkcia prevedie na prenosovú funkciu digitálneho filtra.

Tým bola odstránená nevýhoda spojená s deformáciou fázovej odozvy analógového prototypu.

Metóda bilineárnej transformácie úplne eliminuje vplyv aliasingu frekvenčnej odozvy a nevyžaduje zvýšenie vzorkovacej frekvencie na zníženie chýb reprodukcie frekvenčnej odozvy. Metóda sa používa, keď nie je potrebná zvýšená presnosť reprodukcie frekvenčnej odozvy analógového prototypu.

Príklad použitia metódy bilineárnej transformácie

Nech je prenosová funkcia analógového prototypu opísaná výrazom:

.

Ak vezmeme do úvahy výraz (4.10), môžeme získať nasledujúci výraz pre prenosovú funkciu požadovaného digitálneho filtra:

,

Kde ;

28 strán (súbor Word)

Zobraziť všetky stránky

Fragment textu diela

MINISTERSTVO INFORMAČNÝCH TECHNOLÓGIÍ A KOMUNIKÁCIÍ

FEDERÁLNA KOMUNIKAČNÁ AGENTÚRA

CHABAROVSKÝ INŠTITÚT INFOKOMUNIKÁCIÍ

(POBOČKA) GOU VPO SIBÍRSKY ŠTÁT

UNIVERZITA TELEKOMUNIKÁCIÍ A INFORMAČNEJ VEDY

KURZOVÁ PRÁCA

o matematických základoch číslicového spracovania

signály

Téma: Výpočet rekurzívneho digitálneho filtra

Špecialita 210405

Rádiokomunikácia, rozhlasové vysielanie a televízia

Možnosť č. 30

Dokončené

Projektový manažér

Hlava oddelenie

Chabarovsk

	Technická úloha	3
	Počiatočné údaje pre možnosť č. 30	4
	Úvod	5
1	Grafické znázornenie úlohy	6
1.1	Metódy navrhovania rekurzívnych digitálnych filtrov	7
1.2	Metódy numerickej integrácie	8
1.3	Metóda invariantnosti impulznej odozvy	10
1.4	Metóda bilineárnej transformácie	12
1.5	Zovšeobecnená binomická transformácia	13
2.	Výpočet prenosovej funkcie analógového filtra a jej prevod na prenosovú funkciu digitálneho filtra	14
3.	Bloková schéma digitálneho filtra	22
4.	Metódy implementácie digitálneho filtra	23
4.1	Hardvérová metóda	23
4.2	Softvérová metóda	24
4.3	Hardvérovo-softvérová metóda	25
	Záver	27
	Bibliografia	28

TECHNICKÁ ÚLOHA

Na základe počiatočných údajov je potrebné vypočítať rekurzívny digitálny filter.

Nasledujúce parametre sa považujú za špecifikované:

1 Typ filtra: dolnopriepustný filter, hornopriepustný filter.

2 Typ filtra: Butterworth (B) alebo Chebyshev (C).

3 Vzorkovacia frekvencia fd.

4 limity šírky pásma (PB):

Horná hranica priepustného pásma fп pre dolnopriepustný filter;

Dolná hranica priepustného pásma fп pre hornopriepustný filter;

5 Hranice zadržiavacích pruhov (DP);

Dolná hranica PV fz pre dolnopriepustný filter;

Horná hranica PV fz pre hornopriepustný filter.

6 Prípustná nerovnomernosť amplitúdovo-frekvenčnej odozvy v PP ∆A max, dB.

7 Minimálny prípustný útlm v PZ A min, dB.

VÝCHOZÍ ÚDAJE PRE VARIANTU č. 30

Typ dolnopriepustného filtra

Typ filtra Butterworth

Vzorkovacia frekvencia fd = 16 kHz

Limity šírky pásma fп = 1,7 kHz

Limity stop pásma fз = 3,8 kHz

Prípustná nerovnosť PP ∆A max = 1,35 dB

Prípustný útlm voľnej zóny A min = 25 dB.

Učiteľ___________ Študent___ ____________

„__27__“ _______máj_______ 2011

ÚVOD

Vysokokvalitné frekvenčné nerekurzívne digitálne filtre (NCF) majú zvyčajne veľkú šírku okna (operátor polynomiálneho filtra). Čím menšia je prípustná šírka prechodovej zóny frekvenčnej odozvy filtra medzi priepustným a potlačovacím pásmom, tým väčšie je filtračné okno. Alternatívnym riešením je použitie rekurzívnych digitálnych filtrov (RDF), pri ktorých je možné počet koeficientov filtra v porovnaní s NDF znížiť o niekoľko rádov.

Rekurzívne filtre majú určitú „pamäť“ založenú na hodnotách predchádzajúcich vzoriek, ktoré môžu byť v limite nekonečné. Vzhľadom na tento faktor sa rekurzívne filtre nazývajú filtre s nekonečnou impulznou odozvou (IIR filtre), na rozdiel od nerekurzívnych filtrov, ktoré majú vždy konečnú impulznú odozvu (FIR filtre). Odozva rekurzívneho filtra na signál zohľadňujúci „pamäť“ vylučuje možnosť vytvárania filtrov s rovnomernou impulznou odozvou a frekvenčné charakteristiky rekurzívnych filtrov sú vždy zložité. Návrh rekurzívnych frekvenčných filtrov s danými frekvenčnými charakteristikami sa vykonáva pomocou z-transformácií.

1. Grafické znázornenie problému

Poďme graficky zobraziť požiadavky na frekvenčnú odozvu dolnopriepustného filtra; na to budete musieť vypočítať:

Obrázok 1 – Frekvenčná charakteristika Butterworthovho filtra a frekvenčná charakteristika filtra

Butterworth v Db.

1.1. Metódy navrhovania rekurzívnych digitálnych filtrov

Prenosová funkcia digitálnych IIR filtrov je daná vzťahom , ktorá je podobná funkcii prenosu AF pri nahradení premennej z s. Preto jedným z prístupov k navrhovaniu digitálnych IIR filtrov je previesť funkciu prenosu AF na funkciu prenosu DF. Aby mali CF požadované vlastnosti ako ich AF, musia byť splnené dve podmienky:

1. Pomyselná os s-roviny () bola namapovaná do jednotkovej kružnice v rovine z ( ). Táto podmienka je potrebná na zachovanie frekvenčných charakteristík AF.

2. Ľavá polovica s-roviny () bola zobrazená v z-rovine vo vnútri jednotkového kruhu (). Táto podmienka je potrebná na zachovanie vlastností stability AF.

1.2. Metóda numerickej integrácie

Diferenciálna rovnica popisujúca AF je nahradená diferenčnou rovnicou CF aproximáciou derivácie s niektorými konečnými rozdielmi. Táto operácia vedie k nahradeniu komplexnej premennej s v prenosovej funkcii AF komplexnou premennou z v prenosovej funkcii CF.

Poskytnú rôzne metódy numerickej integrácie rôzne funkcie prechod a teda rôzne výsledné digitálne funkcie. Zoberme si Eulerovu metódu, ktorá aproximuje časovú deriváciu nepretržitá funkcia konečný rozdiel tvaru

, kde T je interval vzorkovania a y(n)=y(nT). Vo forme operátora rovnica dáva

.

Ukážme to túto metódu spĺňa dve vyššie uvedené podmienky:

1. alebo z toho vyplýva pri .

Mestská rozpočtová vzdelávacia inštitúcia telocvičňa č.9

EXPERIMENTÁLNO-ABSTRAKTNÝ PROJEKT

na túto tému:

Aplikácia metódy invariantov pri riešení úloh Jednotnej štátnej skúšky a olympiády

Vykonané:

zrenica XI"B" trieda

Tiščenko Elina

Vedecký riaditeľ:

učiteľ matematiky

Khatuntseva

Irina Vladimirovna

Voronež – 2017

Obsah

Úvod

V modernej matematike zohráva významnú úlohu pojem invariantnosti, t.j. nemennosť matematického objektu. Mnohé definície matematiky v skutočnosti súvisia s týmto pojmom, hoci samotný pojem invariancia v učebniciach absentuje.

Príklad: dokonca funkciu f(x) s doménou definície R je invariantná, pretože f(x)= f(-x).

Prítomnosť jednej alebo druhej invariantnej vlastnosti v matematickom objekte umožňuje stanoviť niektoré všeobecné kvalitatívne vlastnosti tohto objektu.

Cieľom tejto práce je ukázať využitie invariantnej metódy pri riešení úloh Jednotnej štátnej skúšky a olympiády.

Tejto téme sa venuje množstvo literatúry od popredných univerzít v krajine, ako je Moskovská štátna univerzita a Moskovský inštitút fyziky a technológie. Klasickou knihou o teórii invariantov je kniha vynikajúceho nemeckého matematika Herleana Weyla. A študenti Oxfordskej univerzity každoročne vydávajú časopis „The Invariant“.

Táto téma sa zdá byť veľmi aktuálna, pretože... Invariantná metóda vám umožňuje riešiť problémy celkom jednoducho vyšší levelťažkosti.

Kapitola 1. Aplikácia invarianto metódy pri riešení problémov olympiády

Za invarianty sa najčastejšie považuje parita (nepárna parita), zvyšok po delení, permutácia, sfarbenie atď.

Použitie parity je jednou z najčastejšie sa vyskytujúcich myšlienok pri riešení úloh olympiády. Sformulujme najdôležitejšie tvrdenia, na ktorých je založená aplikácia tejto myšlienky:

parita súčtu niekoľkých celých čísel sa zhoduje s paritou počtu nepárnych členov;

znamienko súčinu viacerých (nenulových) čísel je určené rovnomernosťou počtu záporných faktorov.

Úloha 1.

Na tabuli je napísaných desať plusov a pätnásť mínusov. Je povolené vymazať akékoľvek dva znaky a namiesto nich napísať plus, ak sú rovnaké, a mínus inak. Aký znak zostane na tabuli po vykonaní dvadsiatich štyroch takýchto operácií?

Riešenie.

Každé plus nahraďte číslom1 a každé mínus je číslo-1 .

Potom vymažeme ľubovoľné dve čísla a zapíšeme ich súčin. Preto súčin všetkých čísel napísaných na tabuli zostane nezmenený.

Keďže produkt bol pôvodne negatívny (15 záporné čísla), potom na konci zostanenegatívne.

Odpoveď: mínus.

Úloha 2.

Chlapec dostal zlú známku z matematického testu a v návale zúfalstva roztrhal papier s prácou na desať kúskov. Potom jeden z výsledných kúskov roztrhal na ďalších 10 kusov. Môže byť na konci relaxu 2015 papierikov?

Riešenie.

Zakaždým, keď roztrhne jeden papierik o 10, chlapec zvýši celkový počet papierikov o 9. Po prvom roztrhnutí bude mať 1+9=10 kusov, po druhom - 10+9=19 kusov atď. . To znamená, že počet kusov papiera pri n-tom roztrhnutí je určený vzorcom 1+9n.

Pozrime sa, či je číslo 2015 reprezentovateľné ako 1+9n:

1+9 n=2015;

9 n=2014.

2014 nie je deliteľné 9 bezo zvyšku, preto na konci relaxácie nemôže byť 2015 dielikov.

odpoveď: Nie

Úloha 3.

Tabuľa obsahuje čísla od 1 do 1998. V jednom ťahu môžete vymazať ľubovoľné dve čísla a namiesto nich zapísať ich rozdiel, kým nezostane jedno číslo. Môže byť toto číslo nula?

Riešenie.

Zvážte súčet všetkých čísel napísaných na tabuli pred a po jednom kroku. Môžeme vymazať číslaa, b. Potom sa súčet všetkých čísel najprv rovnal , a potom kdeS– súčet všetkých ostatných čísel. Ako vidíme, náhrada (a+ b) dňa (a- b) nemení paritu súčtu všetkých čísel. Súčet čísel na úplnom začiatku je nepárne číslo (
), čo znamená, že v každom kroku bude súčet čísel napísaných na tabuli nepárny. Nula je párne číslo, takže ju nemôžeme dostať na hraciu plochu.

odpoveď: nie.

Úloha 4.

Každá bunka štvorcového stola 2*2 je natretá čiernou resp biela farba, ako je znázornené na obrázku nižšie. Jedným pohybom môžete prefarbiť bunky v ľubovoľnom riadku, v ľubovoľnom stĺpci alebo v akejkoľvek uhlopriečke: čierne - biele a biele - čierne. Je možné niekoľkými ťahmi získať tabuľku, kde sú všetky bunky biele?

Riešenie.

Priraďme každej bunke 1, ak je natretá bielou farbou, a -1, ak je natretá čiernou farbou. Potom zmena farieb znamená zmenu znakov. Zvážte súčin všetkých čísel zodpovedajúcich bunkám. Keďže pri prefarbovaní meníme znamienka práve dvoch faktorov, súčin všetkých štyroch čísel sa nemení. Na začiatku je tento súčin rovný -1. Požadované zafarbenie zodpovedá produktu rovnému 1. Preto nie je možné prefarbiť tabuľku pomocou uvedených operácií.

odpoveď: nie.

Úloha 5.

Tri kôpky obsahujú 1, 9 a 98 kameňov. V jednom ťahu máte dovolené vziať jeden kameň z ľubovoľných dvoch kôp a presunúť ich na tretiu. Je možné pozbierať všetky kamene na jednej z kôp v niekoľkých ťahoch?

Riešenie.

Zoberme si zvyšky pri delení pôvodných čísel tromi - počtom kameňov v kôpkach. V prvej kôpke je zvyšok 1, v druhej - 0, v tretej - 2. Uvažujme, čo bude ďalej z pohľadu zvyškov, keď kamene posunieme:

Našli sme invariant - po ktorejkoľvek z operácií budú zvyšky rovnaké: 0, 1, 2, len budú inak rozdelené. Ak dokážeme zhromaždiť všetky kamene na jednej kôpke, potom budú zvyšky po delení 3 na všetkých kôpkach rovnaké (rovnajúce sa 0). V dôsledku toho nie je možné pomocou uvedených operácií zhromaždiť všetky kamene na jednu hromadu.

odpoveď: nie.

Úloha 6.

Na rovine je uvedená nepretínajúca sa uzavretá prerušovaná čiara, ktorej žiadne tri vrcholy neležia na tej istej priamke. Nazvime dvojicu nesusediacich prepojení lomenou čiaroušpeciálne, ak pokračovanie jednej z nich pretína druhú. Dokážte, že počet špeciálnych párov je párny.

Riešenie.

Zoberme si susedné spojenia AB a BC a nazvime ichrohu uhol symetrický k uhlu ABC vzhľadom na bod B (na obrázku pod rohom je tieňovaný). Pre všetky vrcholy prerušovanej čiary možno uvažovať o rovnakých rohoch. Je zrejmé, že počet špeciálnych párov sa rovná počtu priesečníkov prepojení s rohmi. Zostáva poznamenať, že počet segmentov prerušovanej čiary pretínajúcich sa s jedným rohom je párny, pretože na ceste z A do C prerušovaná čiara vstupuje do rohu toľkokrát, koľkokrát ho opustí (vyplýva to z podmienky, že žiadne tri vrcholy prerušovanej čiary neležia na tej istej priamke). Preto je počet špeciálnych párov párny, čo sme potrebovali dokázať.

Úloha 7 (krajská etapa celoruskej olympiády školákov, 2016-2017, 11. ročník, druhý deň, č. 8).

Na začiatok sa na stôl položí 100 kariet, na každej je napísané prirodzené číslo; Navyše medzi nimi je presne 28 kariet s nepárnymi číslami. Potom sa každú minútu vykoná ďalší postup. Na každých 12 kariet ležiacich na stole sa vypočíta súčin čísel, ktoré sú na nich napísané, všetky tieto súčiny sa spočítajú a výsledné číslo sa zapíše na novú kartu, ktorá sa pripočíta k tým, ktoré ležia na stole. Je možné zvoliť počiatočných 100 čísel tak, aby pre akékoľvek prirodzené d bola skôr či neskôr karta s číslom deliteľným
?

Riešenie.

Ak je v určitom okamihu medzi číslami na kartách presne k nepárnych čísel, potom medzi súčinmi čísel je presne 12
zvláštny; preto číslo na ďalšej pridanej karte bude nepárne presne vtedy, keď bude nepárne (a potom sa k v tej minúte zvýši o 1).

Je ľahké vidieť, že číslo
nepárne (vyplýva to zo skutočnosti, že mocniny dvoch sú zahrnuté v
A
, sú si rovné). Ďalej, pri postupnej kontrole zistíme, že prvý
,
,
- nepárne čísla a
- dokonca. Keď teda počet nepárnych kariet dosiahne 32, už sa nebude zvyšovať a nepárnych kariet bude na stole vždy len 32 a všetky pridané čísla budú párne.

Nechaj to teraz n-ďalši krok – súčet všetkých súčinov 12 z čísel napísaných na kartičkách, a – súčet všetkých súčinov 11 čísel. číslo
, ktorý bude napísaný na nasledujúcej karte, sa líši od pre súčet súčinov 12 čísel, medzi ktorými je práve pridané párne číslo , t.j. na
. Znamená, . číslo - párne, keďže počet nepárnych súm je 11
dokonca. znamená,
nepárne a maximálna mocnina dvoch, ktorá je deliteľná
rovná maximálnej mocnine dvoch, ktorá je deliteľná . To znamená, že od začiatku neboli na stole žiadne čísla, čo je pre každého prirodzenédboli delené , potom sa už takéto čísla nebudú zobrazovať.

Odpoveď: nie, nemôžete.

Kapitola 2. Aplikácia metódy invariantov v úlohách Unified State Examination obsahujúcich parameter

Po analýze veľké množstvá problémov bol zostavený algoritmus na riešenie problémov s parametrom metódou invariantov.

Algoritmus na riešenie problémov s parametrami pomocou invariantu:

1) skontrolujte nemennosť daná rovnica, nerovnosť, sústava rovníc (nerovnice);

2) nájsť platné hodnoty parameter z kontroly splnenia podmienok: za „symetriu vzhľadom na znamienko premennej“ dosaďte jej nulovú hodnotu; pri „symetrii vzhľadom na permutáciu premenných“ sú všetky premenné označené jedným písmenom;

3) skontrolujte, či zistené hodnoty parametrov spĺňajú podmienky problému;

4) napíšte odpoveď.

Vyhlásenie 1 . Ak výraz
invariantný pod transformácia
a rovnica
má koreň ,To

Vyhlásenie 2. Ak výraz

a rovnica
má riešenie
, potom dvojicu čísel

Vyhlásenie 3 . Ak výraz
transformačný invariant
a rovnica
má riešenie
, potom dvojicu čísel
aj riešenie tejto rovnice.

Vyhlásenie 4. Ak výraz
transformačný invariant
A
a rovnica
má riešenie
, potom pár čísel
aj riešenie tejto rovnice.

Vyhlásenie 5. Ak výraz
transformačný invariant
, rovnica
má koreň , To
aj koreň tejto rovnice.

Úloha 1.

Nájdite všetky hodnoty parametra a, pre ktoré má rovnica jedno riešenie

Riešenie.

Všimnite si, že ak je koreň rovnice, potom - - aj koreň => jeden koreň môže byť iba ak =-=0.
Poďme nahradiť
:

o
:

1 koreň, vhodné

o
:

Ľavá strana táto rovnica je väčšia alebo rovná
, a táto spodná hranica je presná - dosahuje sa pri
. Odhad pravej strany je trochu náročnejší. V prvom rade si všimnite, že pri zmene premennej od
predtým
výraz
sa zmení z -1 na 1. Na segmente
funkciu
zvyšuje monotónne od
predtým
. Preto ten výraz
sa líši od
predtým
. V súlade s tým sa pravá strana rovnice (1) líši od
predtým
a hodnoty na pravej strane rovnice úplne vyplnia tento segment. Zo získaných informácií týkajúcich sa možné hodnoty vľavo a pravé časti z rovnice (1) vyplýva, že sa môžu rovnať len vtedy, keď sú si súčasne rovné
. Inými slovami, rovnica (1) je ekvivalentná systému:

Prvá rovnica má jeden koreň
, čo spĺňa aj druhú rovnicu sústavy. To znamená, že systém a s ním aj pôvodná rovnica má jediné rozhodnutie
. Preto sa kontroluje hodnota parametra (
) musia byť zahrnuté v odpovedi na úlohu.

odpoveď: 0;
.

Úloha 2. systém nerovností
má jediné riešenie?

Riešenie. 1. V tomto systéme pozorujeme „symetriu pri zmene premenných“. Potom, ak je riešenie pre systém, potom
aj riešenie systému. Jedinečnosť riešenia je dosiahnutá pod podmienkou
(Vyhlásenie 4).

2. Označenie všetkých premenných podľa
Z nerovnosti, ktorá má jedinečné riešenie, ak je diskriminant kvadratická trojčlenka rovná nule, tie.

3. Skontrolujeme, či má systém jedinečné riešenie pre nájdené hodnoty parametrov.

a) Nahradíme tento systém nerovnosti
:

Sčítajme nerovnosti posledného systému:
+

Otvorením zátvoriek a uvedením podobných výrazov dostaneme: . Odtiaľ



- jediné rozhodnutie.

b) Pri striedaní
dostaneme jediné riešenie

odpoveď:

Úloha 3. Nájdite všetky hodnoty parametra, pre ktorý je systém rovníc

má štyri rôzne riešenia.

Riešenie.

Z formy systému vyplýva, že > ​​0.

1. Systém je invariantný, keď je nahradený - a na - . Preto ak požadovanú hodnotu parametra a dvojicu čísel ;
- riešenie sústavy, potom dvojice
;
, ;
A
; -
aj systémové riešenia. (Vyhlásenia 2 a 3). Preto nájdeme riešenia pri ≥ 0, ≥0. Ukážme si grafy rovníc v jednom súradnicovom systéme. Graf prvej rovnice - body strán štvorcaA B C D, grafom druhého je kruh so stredom v počiatku a polomerom rovným .

Obrázok ukazuje, že systém má presne štyri riešenia v dvoch prípadoch: 1)


;
; pretože > 0, teda
; 2) = 0 E- polomer kružnice vpísanej do štvorca, ktorého strana sa rovná
podľa Pytagora z trojuholníka BOS.

znamená, 0E =
, potom =
kde 2
= 2; 2 =
a =
.

Odpoveď: = 1; =
.

Úloha 4. Pri akých hodnotách parametrov sústava rovníc
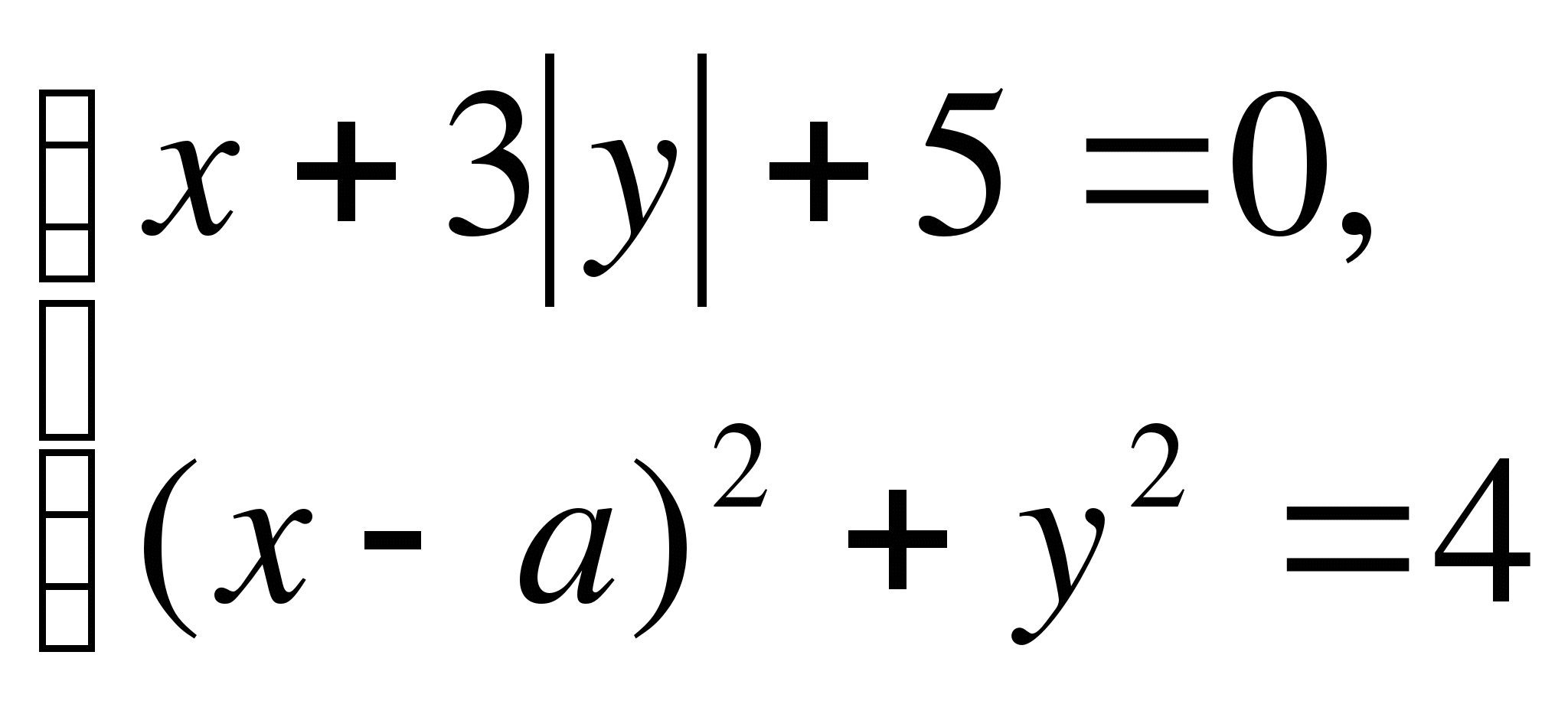má presne tri riešenia?

Riešenie. 1. Ak dvojica čísel ;
- riešenie systému, - požadovaný parameter, potom pár

; -
– tiež riešenie systému. znamená, = -
= 0. (Vyhlásenie 3).

2. Nahradíme = 0 do tohto systému rovníc.

Dostaneme:

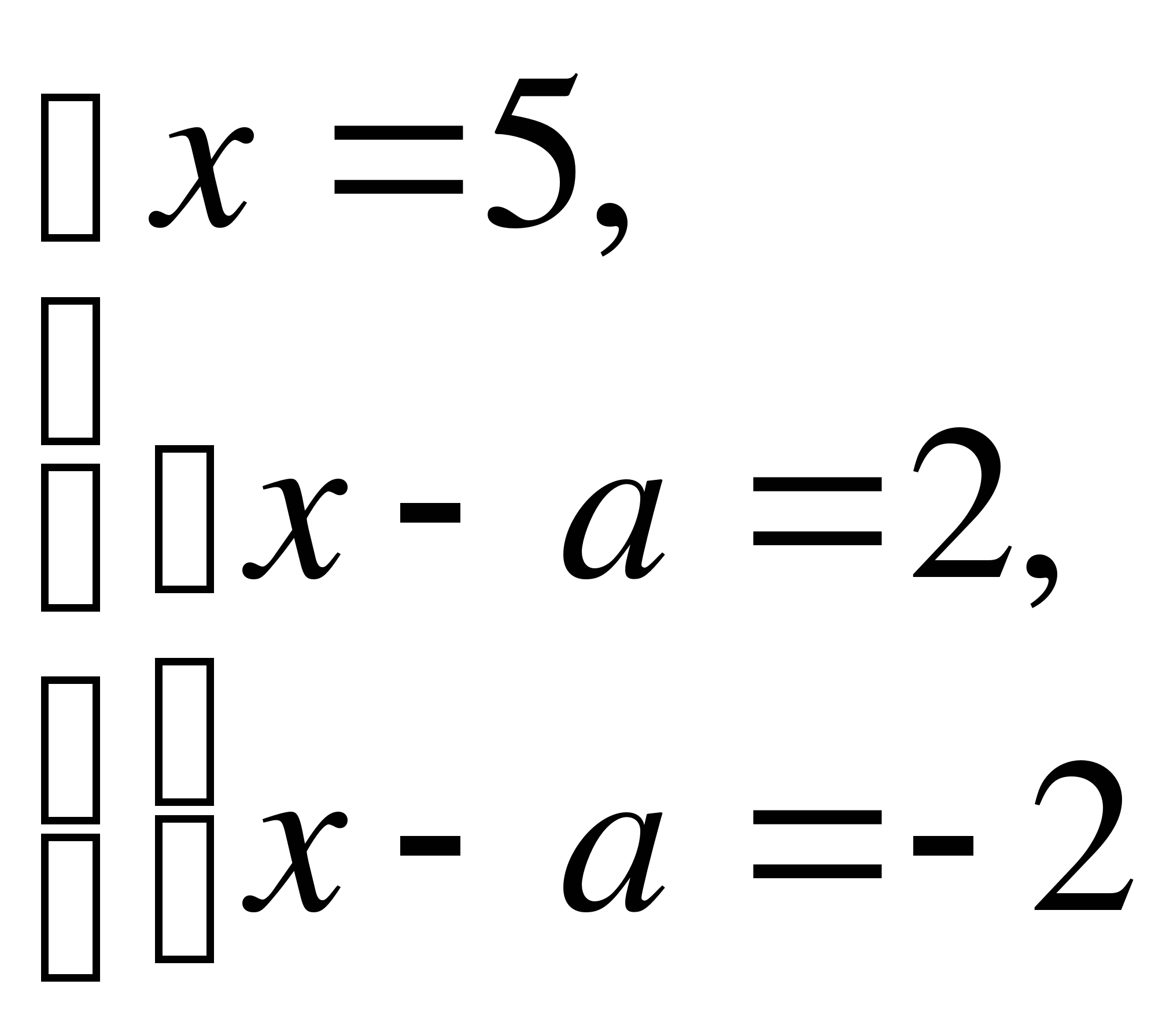
Pozrime sa, či táto rovnica s nájdenými hodnotami má jediné rozhodnutie. o =-3 máme:

Poďme vyriešiť druhú rovnicu systému:

alebo
nemá riešenia.

Ak y=0, potom x=5 a (-5; 0) je jediné riešenie systému. znamená,
nesedí.. Záver

V priebehu práce bola študovaná metóda invariantov. Metóda invariantov bola použitá na riešenie úloh Jednotnej štátnej skúšky s parametrom a olympiádových úloh o vyfarbení, parite, delení zvyškov, odôvodnených a jasne znázornených. praktické využitie metóda.

Zoznam použitej literatúry

INVARIANTNÁ METÓDA RIEŠENIA MATEMATICKÝCH PROBLÉMOV

Ostonov K.

(Samarkand Štátna univerzita)

Pri riešení niektorých matematických úloh sa používa množina transformácií požadovaného objektu a je potrebné pomocou týchto transformácií získať z jedného stavu objektu ďalšiu. Vyčíslením možností si v mnohých prípadoch môžete overiť platnosť odpovede „nie“, ale dokázať správnosť získaného výsledku bude ťažké. Invariantná metóda sa považuje za takú matematickú metódu riešenia takýchto problémov. Najprv si definujme, čo je invariant?

Definícia 1. Invariant je niečo, čo sa pri transformáciách nemení.

Invariant môže byť napríklad číslo, množina čísel, parita čísla atď.

Nehnuteľnosť 1. Ak je hodnota invariantu v dvoch stavoch objektu odlišná, potom jeden z nich nemožno získať od druhého.

V mnohých matematických úlohách sa párnosť (nepárnosť) čísel a zvyšok delenia považujú za invarianty.

Tu je to v prvom rade založené na definícii párneho a nepárneho čísla, abstraktnom koncepte parity, číslach s „rôznymi paritami“, ako aj vlastnosti, že pri pridávaní jedničky sa parita čísel mení. Použitie princípu párneho a nepárneho si vyžaduje použitie nasledujúcich tvrdení:

Vyhlásenie 1. Parita súčtu niekoľkých celých čísel sa zhoduje s paritou počtu nepárnych členov.

Vyhlásenie2. Znamienko súčinu niekoľkých (nie 0) čísel je určené rovnomernosťou počtu záporných faktorov.

Úloha 1. Na papieriku je napísané číslo 11. Šestnásť žiakov si papieriky podáva a každý si k číslu pripočíta jednotku alebo od nej odčíta jednu – ako chce. Mohlo by byť výsledkom číslo 0?

Riešenie. Študenti sú požiadaní, aby vykonali túto operáciu (výsledok každého ťahu je napísaný na tabuľu), zaznamená sa vzor: po každom ťahu sa povaha parity zmení: po prvom študentovi sa číslo stane párnym, po druhom zvláštny; po treťom - párne; po štvrtom - nepárny. Potom po šestnástej bude číslo nepárne. Preto na konci nemôže byť žiadna nula.

Úloha 2. Na vešiaku visí 20 šatiek. Na vešiak sa vystrieda 17 dievčat, ktoré si šatku vyzlečú alebo zavesia. Môže po odchode dievčat zostať presne 10 šatiek?

Riešenie. Po priblížení prvého dievčaťa je počet zostávajúcich šatiek buď 19 alebo 21 (nepárne číslo); potom, čo sa priblíži druhé dievča - buď 18, alebo 20, alebo 22 (párne číslo); potom, čo sa priblíži tretie dievča - buď 17, alebo 21, alebo 23, alebo 19 (nepárne číslo). Po priblížení 17. dievčaťa zostáva nepárny počet šatiek. Ukazuje sa, že ide o protirečenie. To znamená, že nemôže zostať 10 šálov.

Úloha 3. V tabuľke, kde je 15 čísel (-1), môžete vykonať nasledujúcu operáciu: súčasne zmeniť znamienko dvoch (nie viac, nie menej) čísel v tabuľke. Je možné pri použití tejto operácie konečným počtom opakovaní získať tabuľku pozostávajúcu z (+ 1)?

Riešenie. odpoveď: nie. Keďže počet čísel v tabuľke je nepárny a po každej operácii je počet čísel (+ 1) v tabuľke párny. V reči invariantov to znamená: invariant tabuľky vzhľadom na zadanú operáciu je súčinom všetkých čísel v tabuľke. V počiatočnom momente sa tento súčin rovná (- 1) a potrebujeme získať tabuľku, ktorej invariant sa rovná (+ 1).

Úloha 4. Existuje množina čísel. Táto množina čísel sa zmení na trojicu čísel:
,
,
. Daná množina čísel 2016, 2018, 2019. Je možné z nej získať množinu čísiel 2017, 2018, 2019?

Riešenie. odpoveď: nie. Pretože
A
+
+
sú rovnaké, ale súčet 2016+ 2018+ 2019 a súčet 2017+ 2018+ 2019 sú rozdielne.

Úloha 5. Z čísel 2, 3, 4,... 9 vznikli dve prirodzené čísla. Každá číslica bola použitá raz. Môže byť jedno z týchto čísel dvojnásobné?

Riešenie. odpoveď: nie. Nechaj A
– prijaté čísla, S( a) a S( b) – súčet ich číslic. Podľa testu deliteľnosti majú čísla N a S(N) pri delení 3 rovnaké zvyšky. Keďže číslo a+b = 3a je deliteľné 3, potom súčet S = S( a) + S( b) musí byť deliteľné 3, čo je nesprávne, pretože S = 2 + 3 + 4 + … + 9 = 44.

Úloha 6. Čísla 0,1,2,3, …, 9 sú napísané v krúžku. V jednom ťahu môžete pridať rovnaké celé číslo k dvom susedným číslam. Je možné získať desať núl niekoľkými ťahmi?

Riešenie. Je zakázané. Pridanie rovnakých celých čísel k ľubovoľným dvom z daných čísel nezmení paritu celkového súčtu všetkých čísel. Na začiatku je tento súčet 1 + 2 + 3 + … 9 = 45, preto po každom ťahu musí byť celkový súčet získaných čísel nepárny a nula musí byť párne číslo.

Úloha 7. Desať nádob obsahuje 1, 2, 3,..., 10 litrov vody. Z nádoby A do nádoby B je dovolené preliať toľko vody, koľko je v B. Je možné dosiahnuť, aby po niekoľkých transfúziách bolo v 5 nádobách 3 litre a vo zvyšných 6, 7, 8, 9, 10? tie?

Riešenie. Je zakázané. Navrhovaná operácia je semiinvariantná: pri akejkoľvek transfúzii sa počet nepárnych ciev (obsahujúcich nepárny počet litrov vody) nezvyšuje. Počet takýchto ciev klesá pri transfúzii z nepárnej cievy do nepárnej a v ostatných prípadoch sa nemení. Preto je prechod 1, 2, ... 10 - 3, 3, 3, 3, 3, 6, ..., 10 nemožný, pretože zvyšuje počet nepárnych ciev.

Riešenia hádaniek pomocou párnych a nepárnych čísel sa vyznačujú logickou bezchybnosťou a absolútnou platnosťou záverov, ktoré si vyžadujú znalosť najjednoduchších vlastností aritmetických operácií sčítania a odčítania.

Tu platia tieto základné pravidlá parity:

Súčet párnych členov je párny.

Ak je počet nepárnych termínov párny, potom je súčet párny.

Ak je súčet dvoch čísel párne, ich rozdiel je tiež párne číslo.

Ak je súčet dvoch čísel nepárny, ich rozdiel je tiež nepárny.

Ak je počet nepárnych termínov nepárny, potom je nepárny aj súčet.

Ak je jedným z faktorov párne číslo, potom je súčin párny.

Ak sú všetky faktory nepárne, potom je nepárny súčin.

Problém 8. Je číslo 1+2+3+4+…+2000 párne alebo nepárne? Odpoveď: dokonca.

Úloha 9. Je rovnosť 1x2+2x3+3x4+…+99x100 = 20002007 pravdivá? Odpoveď: nie, súčet párnych členov je vždy párny.

Problém 10. .Určite paritu čísel 3(x+1); x+x; x+x+2005, ak je x nepárne. Odpoveď: prvý je párny, druhý je párny, tretí je nepárny.

Problém 11. Dá sa štvorec 25x25 rozrezať na obdĺžniky 1x2? Odpoveď: Nie, číslo 625 nie je deliteľné 2.

Problém 12. Je možné prepojiť 13 miest cestami tak, aby každé mesto malo z neho práve 5 ciest? Odpoveď: nie, každú cestu počítame dvakrát, takže celkový počet ciest musí byť párny. V našom prípade je 13x5 = 65.

Problém 13. Kobylka skáče v priamom smere: prvýkrát o 1 cm, druhýkrát o 2 cm atď. Dokáže sa po 25 skokoch vrátiť na svoje predchádzajúce miesto? Odpoveď: nie, pre návrat na staré miesto musí byť celkový počet centimetrov párny a súčet 1+2+3+...+25 musí byť nepárny.

Problém 14. Je možné zorganizovať šachový turnaj medzi 15 šachistami tak, aby každý hráč odohral 15 partií? Odpoveď: nie, 15x15 je nepárne.

Problém 15. Môže súčin súčtu troch po sebe idúcich prirodzené čísla súčet troch nasledujúcich prirodzených čísel sa rovná 33333? Odpoveď: nie, výrobok musí byť rovnomerný, pretože jedným z faktorov je párne číslo.

Na záver môžeme povedať, že používanie myšlienky párneho a nepárneho umožňuje študentom vyvracanie faktov, na ktore sa pytas, a chapat podobnu logiku ako sposob dokazovania kontradikciou. Pri najčastejšej odpovedi „nemôže“ je potrebné presne vysvetliť, prečo sa to nemôže stať. Ak povie: „Možno,“ stačí uviesť príklad takéhoto usporiadania, distribúcie alebo kombinácie. Okrem priamych problémov rovnosti a nepárnosti môže zahŕňať analýzu problémov, ktoré sú v koncepcii podobné (dva protiklady), vyriešené analýzou priradenia objektu (alebo možnosti) k jednej alebo druhej skupine.

Literatúra

Alkhova Z.N., Makeeva A.V. Mimoškolské aktivity matematiky. – Saratov: „Lýceum“, 2001.

Vilenkin N. Ya. Populárna kombinatorika. - M.: Vzdelávanie, 2003.

Kozlovej E. G. Rozprávky a tipy (úlohy pre matematický krúžok). 2. vydanie, rev. a dodatočné – M.: MTsNMO, 2004.

4. Mednikov L.E. Parity.-M.: MTsNMO, 2009.

5. Babich O.A. Scenár pre mimoškolskú hodinu matematiky (v rámci predmetu laboratórium). 7. ročník. „Invariant“, Kholmsk, 2015.

6. www.strategy48.ru/sites/default/files/fomina1.pdf

anotácia

Tento článok pojednáva o jednej z metód riešenia matematických problémov - o invariantnej metóde, založenej na myšlienke párneho a nepárneho, ako aj o ich špecifickosti pri riešení zábavných problémov v školskom kurze matematiky.

Kľúčové slová : invariant, úloha, myšlienka, parita, číslo, pravidlá, vzor.