Riešenie systémov logaritmických a exponenciálnych nerovníc s lektorom. Zhrnutie lekcie „Racionálne, iracionálne, exponenciálne a trigonometrické nerovnosti“

Všetky úlohy B7, ktoré som kedy videl, boli formulované zhruba rovnakým spôsobom: vyriešte rovnicu. V tomto prípade samotné rovnice patria do jedného z troch typov:

logaritmické;
Orientačné;
Iracionálne.

Všeobecne povedané, plnohodnotný sprievodca každým typom rovnice zaberie viac ako tucet strán, čo ďaleko presahuje rámec jednotnej štátnej skúšky. Preto budeme uvažovať len o najjednoduchších prípadoch, ktoré si vyžadujú jednoduché zdôvodnenie a výpočty. Tieto znalosti budú stačiť na vyriešenie akéhokoľvek problému B7.

V matematike výraz „riešiť rovnicu“ znamená nájsť množinu všetkých koreňov danej rovnice alebo dokázať, že táto množina je prázdna. Čísla však môžete zadať iba do formulára jednotnej štátnej skúšky – žiadne sady. Ak sa teda v úlohe B7 nachádzal viac ako jeden koreň (alebo naopak žiadny), v riešení sa stala chyba.

Logaritmické rovnice

Logaritmická rovnica je akákoľvek rovnica, ktorá sa redukuje na log tvaru a f(X) = k, Kde a > 0, a≠ 1 — logaritmický základ, f(X) je ľubovoľná funkcia, k- nejaký stály.

Táto rovnica je vyriešená zavedením konštanty k pod znak logaritmu: k=log a a k. Základ nového logaritmu sa rovná základni pôvodného logaritmu. Získame rovnicu log a f(X) = log a a k, čo sa rieši vypustením logaritmu.

Všimnite si, že podľa podmienok a> 0, teda f(X) = a k> 0, t.j. pôvodný logaritmus existuje.

Úloha. Riešte rovnicu: log 7 (8 − X) = 2.

Riešenie. log 7 (8 - X) = 2 ⇔ log 7 (8 − X) = log 7 7 2 ⇔ 8 − X = 49 ⇔ X = −41.

Úloha. Riešte rovnicu: log 0,5 (6 − X) = −2.

Riešenie. log 0,5 (6 - X) = −2 ⇔ log 0,5 (6 − X) = log 0,5 0,5 −2 ⇔ 6 − X = 4 ⇔ X = 2.

Ale čo keď sa ukáže, že pôvodná rovnica je zložitejšia ako štandardný log a f(X) = k? Potom ho zredukujeme na štandard, pričom zhromažďujeme všetky logaritmy na jednej strane a čísla na druhej strane.

Ak je v pôvodnej rovnici viac ako jeden logaritmus, budete musieť hľadať oblasť prijateľné hodnoty(ODZ) každej funkcie pod logaritmom. V opačnom prípade sa môžu objaviť ďalšie korene.

Úloha. Vyriešte rovnicu: log 5 ( X+ 1) + denník 5 ( X + 5) = 1.

Pretože v rovnici sú dva logaritmy, nájdeme ODZ:

X + 1 > 0 ⇔ X > −1
X + 5 > 0 ⇔ X > −5

Zistíme, že ODZ je interval (−1, +∞). Teraz riešime rovnicu:

denník 5 ( X+ 1) + denník 5 ( X+ 5) = 1 ⇒ log 5 ( X + 1)(X+ 5) = 1 ⇔ log 5 ( X + 1)(X+ 5) = log 5 5 1 ⇔ ( X + 1)(X + 5) = 5 ⇔ X 2 + 6X + 5 = 5 ⇔ X (X + 6) = 0 ⇔ X 1 = 0, X 2 = −6.

ale X 2 = −6 nespĺňa podmienky pre DL. Čo zostáva, je koreň X 1 = 0.

Exponenciálne rovnice

Exponenciálna rovnica je akákoľvek rovnica, ktorá sa redukuje na tvar a f(X) = k, Kde a > 0, a≠ 1 – základ titulu, f(X) je ľubovoľná funkcia, k- nejaký stály.

Táto definícia takmer doslovne opakuje definíciu logaritmickej rovnice. Exponenciálne rovnice sa riešia ešte jednoduchšie ako logaritmické, pretože tu nie je potrebná funkcia f(X) bol pozitívny.

Aby sme to vyriešili, urobíme náhradu k = a t, Kde t- všeobecne povedané, logaritmus ( t=log a k), ale v Jednotnej štátnej skúške čísla a A k sa vyberie tak, aby ste našli t bude to jednoduché. Vo výslednej rovnici a f(X) = a t základy sú rovnaké, čo znamená, že ukazovatele sú rovnaké, t.j. f(X) = t. Riešenie poslednej rovnice zvyčajne nespôsobuje problémy.

Úloha. Riešte rovnicu: 7 X − 2 = 49.

Riešenie. 7 X − 2 = 49 ⇔ 7 X − 2 = 7 2 ⇔ X − 2 = 2 ⇔ X = 4.

Úloha. Vyriešte rovnicu: 6 16 − X = 1/36.

Riešenie. 6 16 − X = 1/36 ⇔ 6 16 − X = 6 −2 ⇔ 16 − X = −2 ⇔ X = 18.

Trochu o transformácii exponenciálnych rovníc. Ak sa pôvodná rovnica líši od a f(X) = k , aplikujeme pravidlá pre prácu so stupňami:

a n · a m = a n + m ,
a n / a m = a n − m ,
(a n) m = a n · m .

Okrem toho musíte poznať pravidlá nahradenia koreňov a zlomkov mocninami s racionálnym exponentom:

Takéto rovnice sú v Jednotnej štátnej skúške extrémne zriedkavé, ale bez nich by bola analýza problému B7 neúplná.

Úloha. Vyriešte rovnicu: (5/7) X− 2 · (7/5) 2 X − 1 = 125/343

Všimni si:

(7/5) 2X − 1 = ((5/7) −1) 2X − 1 = (5/7) 1 − 2X ,
125/343 = (5 3) /(7 3) = (5/7) 3 .

Máme: (5/7) X− 2 · (7/5) 2 X − 1 = 125/343 ⇔ (5/7) X− 2 · (5/7) 1 − 2 X = (5/7) 3 ⇔ (5/7) X − 2 + 1 − 2X = (5/7) 3 ⇔ (5/7) −X − 1 = (5/7) 3 ⇔ −X − 1 = 3 ⇔ X = −4.

Iracionálne rovnice

Iracionálnou rozumieme akúkoľvek rovnicu obsahujúcu odmocninu. Z celej škály iracionálnych rovníc budeme uvažovať iba o najjednoduchšom prípade, keď má rovnica tvar:

Aby sme túto rovnicu vyriešili, odmocnime obe strany. Dostaneme rovnicu f(X) = a 2. V tomto prípade je požiadavka ODZ automaticky splnená: f(X) ≥ 0, pretože a 2 ≥ 0. Zostáva vyriešiť jednoduchú rovnicu f(X) = a 2 .

Úloha. Vyriešte rovnicu:

Obidve strany odmocníme a dostaneme: 5 X − 6 = 8 2 ⇔ 5X − 6 = 64 ⇔ 5X = 70 ⇔ X = 14.

Úloha. Vyriešte rovnicu:

Najprv, ako minule, obe strany uvaľujeme. A potom pridajte do čitateľa znamienko mínus. Máme:

Všimnite si, že kedy X= −4 pod odmocninou bude kladné číslo, t.j. Požiadavka ODZ bola splnená.

Do absolvovania jednotnej štátnej skúšky z matematiky zostáva stále menej času. Situácia sa vyostruje, nervy školákov, rodičov, učiteľov a vychovávateľov sú čoraz napätejšie. Vzlietnuť nervové napätie Denné hĺbkové hodiny matematiky vám pomôžu. Koniec koncov, nič, ako vieme, vás nenabíja pozitivitou a nepomôže vám zložiť skúšky ako dôvera vo vaše schopnosti a vedomosti. Dnes vám učiteľ matematiky povie o riešení systémov logaritmických a exponenciálnych nerovností, úloh, ktoré tradične spôsobujú ťažkosti mnohým moderným stredoškolákom.

Aby ste sa ako lektor matematiky naučili riešiť úlohy C3 z Jednotnej štátnej skúšky z matematiky, odporúčam vám venovať pozornosť nasledujúcim dôležitým bodom.

1. Predtým, ako začnete riešiť systémy logaritmických a exponenciálnych nerovností, musíte sa naučiť, ako riešiť každý z týchto typov nerovností samostatne. Najmä na pochopenie toho, ako sa nachádza rozsah prijateľných hodnôt, sa vykonávajú ekvivalentné transformácie logaritmických a exponenciálnych výrazov. Niektoré tajomstvá, ktoré s tým súvisia, môžete pochopiť preštudovaním článkov „“ a „“.

2. Zároveň je potrebné si uvedomiť, že nie vždy riešenie sústavy nerovníc spočíva v riešení každej nerovnosti samostatne a pretínaní výsledných intervalov. Niekedy, keď poznáme riešenie jednej nerovnosti systému, riešenie druhej sa stáva oveľa jednoduchším. Ako učiteľ matematiky, ktorý pripravuje školákov na záverečné skúšky vo formáte Jednotnej štátnej skúšky, odhalím v tomto článku niekoľko tajomstiev, ktoré s tým súvisia.

3. Je potrebné jasne pochopiť rozdiel medzi priesečníkom a zjednotením množín. Ide o jeden z najdôležitejších matematických poznatkov, ktorý sa skúsený profesionálny lektor snaží dať svojmu študentovi už od prvých hodín. Vizuálne znázornenie prieniku a spojenia množín je dané takzvanými „Eulerovými kruhmi“.

Priesečník množín je množina, ktorá obsahuje len tie prvky, ktoré má každá z týchto množín.

križovatka

Znázornenie priesečníka množín pomocou „eulerovských kruhov“

Vysvetlenie na dosah ruky. Diana má v kabelke „súpravu“ pozostávajúcu z ( perá, ceruzka, vládcov, zošity, hrebene). Alice má v kabelke „súpravu“ pozostávajúcu z ( notebook , ceruzka, zrkadlá, zošity, kyjevské kotlety). Priesečníkom týchto dvoch „množín“ bude „množina“ pozostávajúca z ( ceruzka, zošity), keďže Diana aj Alice majú oba tieto „prvky“.

Dôležité mať na pamäti! Ak je riešením nerovnosti interval a riešením nerovnosti je interval, potom riešením systémov je:

je interval, ktorý je križovatka pôvodné intervaly. Tu a ďalej nižšieznamená ktorýkoľvek zo znakov title="Rendered by QuickLaTeX.com" height="17" width="93" style="vertical-align: -4px;">!} a pod - je to opačné znamenie.

Spojenie množín je súprava, ktorá pozostáva zo všetkých prvkov pôvodných súprav.

Inými slovami, ak sú dané dve sady a potom ich zjednotenie bude súbor nasledujúceho formulára:

Zobrazenie zjednotenia množín pomocou „eulerovských kruhov“

Vysvetlenie na dosah ruky. Spojenie „množín“ v predchádzajúcom príklade bude „množinou“ pozostávajúcou z ( perá, ceruzka, vládcov, zošity, hrebene, notebook, zrkadlá, kyjevské kotlety), keďže pozostáva zo všetkých prvkov pôvodných „súborov“. Jedno objasnenie, ktoré nemusí byť zbytočné. Kopa nemôže obsahujú rovnaké prvky.

Dôležité mať na pamäti! Ak je riešením nerovnosti interval a riešením nerovnosti je interval, potom riešením populácie je:

je interval, ktorý je únie pôvodné intervaly.

Prejdime priamo k príkladom.

Príklad 1 Vyriešte systém nerovností:

Riešenie úlohy C3.

1. Najprv vyriešime prvú nerovnosť. Pomocou substitúcie prejdeme k nerovnosti:

2. Teraz vyriešme druhú nerovnosť. Rozsah jeho prípustných hodnôt je určený nerovnosťou:

Title="Rendered by QuickLaTeX.com">!}

V rozsahu prijateľných hodnôt, berúc do úvahy, že základ logaritmu title="Rendered by QuickLaTeX.com" height="18" width="52" style="vertical-align: -4px;"> переходим к равносильному неравенству:!}

Vylúčením riešení, ktoré nie sú v rámci prijateľných hodnôt, dostaneme interval

3. Odpovedať systém budú nerovnosti križovatka

Výsledné intervaly na číselnej osi. Riešením je ich priesečník

Príklad 2 Vyriešte systém nerovností:

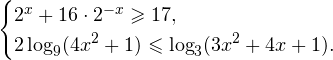
Riešenie úlohy C3.

1. Najprv vyriešme prvú nerovnosť. Vynásobte obe časti názvom title="Rendered by QuickLaTeX.com" height="14" width="55" style="vertical-align: 0px;"> и делаем замену в результате чего приходим к неравенству:!}

Prejdime k reverznej substitúcii:

Title="Rendered by QuickLaTeX.com">!}

Grafické znázornenie výsledného intervalu. Riešením systému je ich priesečník

Príklad 3 Vyriešte systém nerovností:

Riešenie úlohy C3.

1. Najprv vyriešme prvú nerovnosť. Vynásobte obe časti názvom title="Rendered by QuickLaTeX.com" height="18" width="61" style="vertical-align: -4px;"> после чего получаем неравенство:!}

Pomocou substitúcie sa dostaneme k nasledujúcej nerovnosti:

Prejdime k reverznej substitúcii:

2. Teraz vyriešme druhú nerovnosť. Najprv určme rozsah prijateľných hodnôt tejto nerovnosti:

ql-right-eqno">

Vezmite prosím na vedomie, že

Potom, berúc do úvahy rozsah prijateľných hodnôt, dostaneme:

3. nachádzame všeobecné riešenia nerovnosti Porovnanie získaných iracionálnych hodnôt uzlových bodov je úlohou v v tomto príklade nie je v žiadnom prípade triviálne. Môžete to urobiť nasledovne. Pretože

Title="Rendered by QuickLaTeX.com">!}

To a konečná odpoveď systému vyzerá takto:

Príklad 4. Vyriešte systém nerovností:

Riešenie úlohy C3.

1. Najprv vyriešme druhú nerovnosť:

2. Prvá nerovnosť pôvodného systému je logaritmická nerovnosť s premenlivým základom. Pohodlný spôsob riešenia takýchto nerovností je opísaný v článku „Komplexné logaritmické nerovnosti“ a je založený na jednoduchom vzorci:

Znamienko môže byť nahradené ľubovoľným znakom nerovnosti, hlavné je, že je v oboch prípadoch rovnaké. Použitie tohto vzorca výrazne zjednodušuje riešenie nerovnosti:

Poďme teraz určiť rozsah prijateľných hodnôt tejto nerovnosti. Nastavuje sa nasledujúcim systémom:

Title="Rendered by QuickLaTeX.com">!}

Je ľahké vidieť, že tento interval bude zároveň riešením našej nerovnosti.

3. Konečná odpoveď na originál systémov budú nerovnosti križovatka výsledné intervaly, tzn

Príklad 5. Vyriešte systém nerovností:

Riešenie úlohy C3.

1. Najprv vyriešme prvú nerovnosť. Použijeme substitúciu a pristúpime k nasledujúcej kvadratickej nerovnosti:

2. Teraz vyriešme druhú nerovnosť. Rozsah jeho prípustných hodnôt je určený systémom:

Title="Rendered by QuickLaTeX.com">!}

Táto nerovnosť je ekvivalentná nasledujúcemu zmiešanému systému:

V rozsahu prijateľných hodnôt, to znamená s title="Rendered by QuickLaTeX.com" height="18" width="53" style="vertical-align: -4px;"> используя равносильные преобразования переходим к следующей смешанной системе:!}

Ak vezmeme do úvahy rozsah prijateľných hodnôt, získame:

3. Konečné rozhodnutie originálu systémov je

Riešenie úlohy C3.

1. Najprv vyriešme prvú nerovnosť. Pomocou ekvivalentných transformácií ho privedieme do tvaru:

2. Teraz vyriešme druhú nerovnosť. Rozsah jeho platných hodnôt je určený intervalom: title="Rendered by QuickLaTeX.com" height="14" width="68" style="vertical-align: 0px;"> Используя замену переменной переходим к следующему квадратичному неравенству:!}

Táto odpoveď úplne patrí do rozsahu prijateľných hodnôt nerovnosti.

3. Pretínaním intervalov získaných v predchádzajúcich odsekoch získame konečnú odpoveď na systém nerovností:

Dnes sme riešili systémy logaritmických a exponenciálnych nerovníc. Úlohy tohto druhu boli ponúkané v skúšobných verziách Jednotnej štátnej skúšky z matematiky počas celého súčasného školský rok. Ako lektor matematiky so skúsenosťami s prípravou na Jednotnú štátnu skúšku však môžem povedať, že to neznamená, že podobné úlohy budú skutočné možnosti Jednotná štátna skúška z matematiky v júni.

Dovoľte mi vysloviť jedno varovanie, určené predovšetkým tútorom a učiteľom škôl, ktorí pripravujú stredoškolákov na vykonanie Jednotnej štátnej skúšky z matematiky. Je veľmi nebezpečné pripravovať školákov na skúšku striktne z daných tém, pretože v tomto prípade hrozí úplné „neúspech“ aj pri miernej zmene predtým uvedeného formátu úloh. Matematické vzdelanie musí byť úplné. Vážení kolegovia, neprirovnávajte svojich študentov k robotom takzvaným „školením“ na riešenie určitého typu problémov. Nie je predsa nič horšie ako formalizácia ľudského myslenia.

Veľa šťastia a tvorivého úspechu všetkým!

Sergej Valerijevič

Ak sa pokúsite, existujú dve možnosti: bude to fungovať alebo to nebude fungovať. Ak to neskúsite, je len jeden.
© Ľudová múdrosť

Riešenie väčšiny matematických problémov jedným alebo druhým spôsobom zahŕňa transformáciu numerických, algebraických alebo funkčných výrazov. Uvedené platí najmä pre rozhodnutie. Vo verziách Jednotnej štátnej skúšky z matematiky tento typ úloh zahŕňa najmä úlohu C3. Naučiť sa riešiť úlohy C3 je dôležité nielen za účelom úspešné ukončenie Jednotná štátna skúška, ale aj z toho dôvodu, že táto zručnosť bude užitočná pri štúdiu matematického kurzu na vysokej škole.

Pri plnení úloh C3 sa musíte rozhodnúť rôzne druhy rovnice a nerovnice. Medzi nimi sú racionálne, iracionálne, exponenciálne, logaritmické, trigonometrické, obsahujúce moduly (absolútne hodnoty), ako aj kombinované. Tento článok sa zaoberá hlavnými typmi exponenciálnych rovníc a nerovníc, ako aj rôzne metódy ich rozhodnutia. Prečítajte si o riešení iných typov rovníc a nerovníc v časti „“ v článkoch venovaných metódam riešenia úloh C3 z r. Možnosti jednotnej štátnej skúšky matematiky.

Než začneme analyzovať konkrétne exponenciálne rovnice a nerovnice, ako učiteľ matematiky vám navrhujem oprášiť nejaký teoretický materiál, ktorý budeme potrebovať.

Exponenciálna funkcia

Čo je to exponenciálna funkcia?

Funkcia formulára r = a x, Kde a> 0 a a≠ 1 sa volá exponenciálna funkcia.

Základné vlastnosti exponenciálnej funkcie r = a x:

Graf exponenciálnej funkcie

Graf exponenciálnej funkcie je exponent:

Grafy exponenciálnych funkcií (exponentov)

Riešenie exponenciálnych rovníc

Orientačné sa nazývajú rovnice, v ktorých sa neznáma premenná nachádza len v exponentoch niektorých mocnín.

Pre riešenia exponenciálne rovnice musíte poznať a vedieť používať nasledujúcu jednoduchú vetu:

Veta 1. Exponenciálna rovnica a f(X) = a g(X) (Kde a > 0, a≠ 1) je ekvivalentná rovnici f(X) = g(X).

Okrem toho je užitočné zapamätať si základné vzorce a operácie so stupňami:

Title="Rendered by QuickLaTeX.com">!}

Príklad 1 Vyriešte rovnicu:

Riešenie: Používame vyššie uvedené vzorce a substitúciu:

Rovnica potom znie:

Diskriminujúci prijatých kvadratická rovnica pozitívne:

Title="Rendered by QuickLaTeX.com">!}

Znamená to, že daná rovnica má dva korene. Nájdeme ich:

Ak prejdeme na spätnú substitúciu, dostaneme:

Druhá rovnica nemá korene, pretože exponenciálna funkcia je striktne kladná v celej oblasti definície. Vyriešme to druhé:

Berúc do úvahy to, čo bolo povedané vo vete 1, prejdeme k ekvivalentnej rovnici: X= 3. Toto bude odpoveď na úlohu.

odpoveď: X = 3.

Príklad 2 Vyriešte rovnicu:

Riešenie: Rovnica nemá žiadne obmedzenia na rozsah prípustných hodnôt, pretože radikálny výraz má zmysel pre akúkoľvek hodnotu X(exponenciálna funkcia r = 9 4 -X kladné a nerovnajúce sa nule).

Rovnicu riešime ekvivalentnými transformáciami pomocou pravidiel násobenia a delenia mocnin:

Posledný prechod sa uskutočnil v súlade s vetou 1.

odpoveď:X= 6.

Príklad 3 Vyriešte rovnicu:

Riešenie: obe strany pôvodnej rovnice možno deliť 0,2 X. Tento prechod bude ekvivalentný, pretože tento výraz je väčší ako nula pre akúkoľvek hodnotu X(exponenciálna funkcia je vo svojej oblasti definície striktne pozitívna). Potom má rovnica tvar:

odpoveď: X = 0.

Príklad 4. Vyriešte rovnicu:

Riešenie: rovnicu zjednodušíme na elementárnu pomocou ekvivalentných transformácií s použitím pravidiel delenia a násobenia mocnin uvedených na začiatku článku:

Delenie oboch strán rovnice 4 X, ako v predchádzajúcom príklade, je ekvivalentná transformácia, pretože tento výraz sa pre žiadne hodnoty nerovná nule X.

odpoveď: X = 0.

Príklad 5. Vyriešte rovnicu:

Riešenie: funkciu r = 3X, stojaci na ľavej strane rovnice, sa zvyšuje. Funkcia r = —X-2/3 na pravej strane rovnice klesá. To znamená, že ak sa grafy týchto funkcií pretínajú, tak maximálne jeden bod. V tomto prípade je ľahké uhádnuť, že grafy sa v bode pretínajú X= -1. Iné korene nebudú.

odpoveď: X = -1.

Príklad 6. Vyriešte rovnicu:

Riešenie: rovnicu zjednodušujeme pomocou ekvivalentných transformácií, pričom máme všade na pamäti, že exponenciálna funkcia je striktne väčšia ako nula pre akúkoľvek hodnotu X a pomocou pravidiel na výpočet súčinu a kvocientu mocnin uvedených na začiatku článku:

odpoveď: X = 2.

Riešenie exponenciálnych nerovností

Orientačné sa nazývajú nerovnice, v ktorých je neznáma premenná obsiahnutá len v exponentoch niektorých mocnín.

Pre riešenia exponenciálne nerovnosti vyžaduje sa znalosť nasledujúcej vety:

Veta 2. Ak a> 1, potom nerovnosť a f(X) > a g(X) sa rovná nerovnosti rovnakého významu: f(X) > g(X). Ak 0< a < 1, то показательное неравенство a f(X) > a g(X) je ekvivalentná nerovnosti s opačným významom: f(X) < g(X).

Príklad 7. Vyriešte nerovnosť:

Riešenie: Uveďme pôvodnú nerovnosť v tvare:

Vydeľme obe strany tejto nerovnosti 3 2 X, v tomto prípade (vzhľadom na pozitívnosť funkcie r= 3 2X) znak nerovnosti sa nezmení:

Použime náhradu:

Potom bude mať nerovnosť tvar:

Takže riešením nerovnosti je interval:

prechodom na opačnú substitúciu dostaneme:

Vďaka kladnosti exponenciálnej funkcie je ľavá nerovnosť splnená automaticky. Využiť známa vlastnosť logaritmus, prejdeme na ekvivalentnú nerovnosť:

Keďže základom stupňa je číslo väčšie ako jedna, ekvivalentom (podľa vety 2) je prechod na nasledujúcu nerovnosť:

Tak sa konečne dostávame odpoveď:

Príklad 8. Vyriešte nerovnosť:

Riešenie: Pomocou vlastností násobenia a delenia mocnín prepíšeme nerovnosť do tvaru:

Predstavme si novú premennú:

Ak vezmeme do úvahy túto substitúciu, nerovnosť má tvar:

Vynásobením čitateľa a menovateľa zlomku číslom 7 dostaneme nasledujúcu ekvivalentnú nerovnosť:

Nasledujúce hodnoty premennej teda spĺňajú nerovnosť t:

Potom, keď prejdeme na opačnú substitúciu, dostaneme:

Pretože základ stupňa je tu väčší ako jedna, prechod na nerovnosť bude ekvivalentný (podľa vety 2):

Konečne sa dostávame odpoveď:

Príklad 9. Vyriešte nerovnosť:

Riešenie:

Obe strany nerovnosti delíme výrazom:

Je vždy väčšia ako nula (kvôli kladnosti exponenciálnej funkcie), takže nie je potrebné meniť znamienko nerovnosti. Dostaneme:

t sa nachádza v intervale:

Ak prejdeme k reverznej substitúcii, zistíme, že pôvodná nerovnosť sa rozdelí na dva prípady:

Prvá nerovnosť nemá riešenia kvôli kladnosti exponenciálnej funkcie. Vyriešme to druhé:

Príklad 10. Vyriešte nerovnosť:

Riešenie:

Vetvy paraboly r = 2X+2-X 2 smerujú nadol, preto je zhora obmedzená hodnotou, ktorú dosahuje vo svojom vrchole:

Vetvy paraboly r = X 2 -2X+2 v ukazovateli smeruje nahor, čo znamená, že je zdola obmedzený hodnotou, ktorú dosiahne vo svojom vrchole:

Zároveň sa ukazuje, že funkcia je ohraničená aj zdola r = 3 X 2 -2X+2, čo je na pravej strane rovnice. Dosahuje svoj cieľ najnižšia hodnota v rovnakom bode ako parabola v exponente a táto hodnota sa rovná 3 1 = 3. Pôvodná nerovnosť teda môže byť pravdivá len vtedy, ak funkcia naľavo a napravo nadobudnú hodnotu rovnajúcu sa 3 v tom istom bode (pri priesečníku Rozsah hodnôt týchto funkcií je iba toto číslo). Táto podmienka je splnená v jediný bod X = 1.

odpoveď: X= 1.

Aby sa naučili rozhodovať exponenciálne rovnice a nerovnice, ich riešenie je potrebné neustále trénovať. S touto neľahkou úlohou vám môžu pomôcť rôzne veci. metodické príručky, problémové knihy zo základnej matematiky, zbierky súťažných úloh, hodiny matematiky v škole, ako aj individuálne hodiny s odborným tútorom. Úprimne vám želám veľa úspechov v príprave a výborné výsledky na skúške.

Sergej Valerijevič

P.S. Vážení hostia! Do komentárov prosím nepíšte požiadavky na riešenie vašich rovníc. Bohužiaľ na to nemám absolútne čas. Takéto správy budú vymazané. Prečítajte si prosím článok. Možno v ňom nájdete odpovede na otázky, ktoré vám nedovolili vyriešiť svoju úlohu sami.

prihláška č.3

Lekcia 225. Racionálne, iracionálne, demonštratívne a trigonometrické nerovnosti.

Dátum:

Typ lekcie: lekciu zovšeobecňovania a systematizácie vedomostí na túto tému.

Ciele lekcie:

zovšeobecnenie poznatkov o spôsoboch riešenia exponenciálnych nerovností. príprava na jednotnú štátnu skúšku;

formovanie adekvátnej sebaúcty a vzájomného hodnotenia u žiakov pri práci v skupine;

rozvoj matematickej reči pri komentovaní riešení, pri zostavovaní algoritmov na dokončenie úlohy; schopnosť prekonávať ťažkosti, schopnosť pracovať s referenčnou literatúrou;

vzdelávanie vzájomnej pomoci.

Vedomosti, schopnosti, zručnosti a vlastnosti, ktoré budú aktualizované/nadobudnuté/upevnené/atď. žiaci počas hodiny:

systematizovať svoje vedomosti o tejto téme;

upevniť teoretické vedomosti o tejto téme;

aplikovať poznatky v neštandardnej situácii.

Potrebné vybavenie a materiály:

Notebooky na individuálne testovanie, multimediálny projektor;

prezentácia na lekciu;

písacie potreby, letáky, hárky na sebahodnotenie.

Vyučovacie metódy: technológia problémovo-situačného učenia s využitím prípadovej fázy.

Kroky lekcie:

1.Org moment - 1 minúta

2. formulácia témy a cieľov vyučovacej hodiny 1 minúta

3. Aktualizácia základných vedomostí. Bleskový prieskum. (3 min.)

4. Výsledky bleskového prieskumu – 2 minúty

5. Kontrola domácich úloh. Klasifikácia. 3 minúty

6.Domáca úloha diferencovaného charakteru s právom výberu. 1 minúta

7.Opakovanie teórie a induktora (vykonanie cielenia) 2 min

8. Precvičovanie zručností riešenia. Práca s referenčnou literatúrou. 5 nerovností 10 min

9. Reklama 2 minúty

10. Prestávka. Neznáme problémy – 2 min

11. riešenie týchto úloh 4 minúty

12. Reklamné riešenia nových problémov 4 min

13. Odraz – 2 min

14. Sebaúcta 1 minúta

Pred začiatkom vyučovacej hodiny sa žiaci posadia do určitých radov podľa troch stupňov tréningu. Upozorňujeme, že zručnosti na preberanú tému nepatria medzi povinné požiadavky na prípravu študentov, preto ju so mnou študujú len pripravenejší študenti (skupina 1 a 2).

Účel lekcie. Analyzujte metódy riešenia iracionálnych nerovností priemeru a zvýšená hladina zložitosť, vypracovať referenčné diagramy.

1. fáza lekcie - organizačná (1 min.)

Učiteľ povie žiakom tému hodiny, účel a vysvetlí účel písomiek, ktoré majú na stole.

2. fáza lekcie (5 min.)

Ústna práca za zopakovanie riešenia jednoduchých úloh na tému „Exponent s racionálnym exponentom“

Učiteľ vyzve študentov, aby postupne odpovedali na otázky, pričom svoju odpoveď komentovali s odkazom na zodpovedajúci teoretický fakt.

Mocnina s racionálnym exponentom

Zjednodušte: 1) 12 m 4 /3 m 8

2) 6 s 3/7 + 4 (s 1/7) 3

3) (32 x 2) 1/5 x 3/5

4) 2 4,6a 2 -1,6a

5) 2x 0,2 x -1,2

6) 4 x 3/5 x 1/10

8) 2x 4/5 · 3x 1/5

9) (3x 2/5) 2 + 2x 4/5

10) 3 x 1/2 x 3/2

Vypočítajte: 11) 4 3,2 m 4 -1,2 m, pričom m = 1/4

12) 6 -5,6a 6 3,6a, s a = 1/2

13) 5 27 2/3 - 16 1/4

14) 3 4,4 s 3 - 6,4 s, s c = 1/2

15) 3x 2/5 x 3/5, pričom x = 2

3. fáza lekcie - štúdium Nová téma(20 min.), prednáška

Učiteľ vyzve 3. skupinu žiakov, aby začali pracovať na opakovaní s kartičkami - konzultantmi na tému „Najjednoduchšie goniometrické rovnice"(keďže študovaný materiál má zvýšenú úroveň zložitosti a nie je povinný). Žiaci 3. skupiny sú spravidla žiaci so slabou matematickou prípravou, pedagogicky zanedbaní školáci. Po splnení úlohy sa karty v rámci skupiny vymenia. Pripravenejší študenti začnú analyzovať novú tému.

Pred analýzou metód riešenia iracionálnych nerovností je potrebné študentom pripomenúť základné teoretické fakty, na základe ktorých sa budú budovať podporné schémy pre ekvivalentné prechody. V závislosti od úrovne prípravy študentov to môžu byť buď ústne odpovede na otázky učiteľa, alebo spoločná práca medzi učiteľom a študentmi, ale v každom prípade by sa malo na hodine povedať nasledovné.

Definícia 1. Nerovnice, ktoré majú rovnakú množinu riešení, sa nazývajú ekvivalentné.

Pri riešení nerovníc sa daná nerovnosť väčšinou transformuje na ekvivalentnú.

Napríklad nerovnosť (x - 3)/(x 2 + 1) sú ekvivalentné, pretože majú rovnakú sadu riešení: X. Nerovnosti 2x/(x - 1) 1 a 2x x - 1 nie sú rovnocenné, pretože riešenia prvého sú riešenia x 1 a riešenia druhého sú čísla x -1.

Definícia 2. Oblasť definície nerovnosti je množina hodnôt x, pre ktoré majú obe strany nerovnosti zmysel.

Motivácia. Nerovnosti samy o sebe sú zaujímavé pre štúdium, pretože Práve s ich pomocou sú v symbolickom jazyku napísané najdôležitejšie úlohy pochopenia reality. Nerovnosť často slúži ako dôležitý pomocný nástroj, ktorý umožňuje dokázať alebo vyvrátiť existenciu akýchkoľvek objektov, odhadnúť ich počet a vykonať klasifikáciu. Preto sa s nerovnosťami musíme vyrovnať nie menej často ako s rovnicami.

Definícia. Nerovnosti obsahujúce premennú pod koreňovým znakom sa nazývajú iracionálne.

Príklad 1√ (5 - x)

Aký je rozsah nerovnosti?

Za akých podmienok vytvára kvadratúra oboch strán ekvivalentnú nerovnosť?

√(5 - x) 5 - x -11

Príklad 2√10 + x - x 2 ≥ 2 10 + x - x 2 ≥ 0 10 + x - x 2 ≥ 4

10 + x - x 2 ≥ 4

pretože každé riešenie druhej nerovnosti systému je riešením prvej nerovnosti.

Príklad 3 Riešiť nerovnosti

b) √2x 2 + 5x - 3 ≤ 0 2x 2 + 5x - 3 = 0

Pozrime sa na tri typické príklady, z ktorých bude zrejmé, ako robiť ekvivalentné prechody pri riešení nerovníc, keď očividná transformácia ekvivalentná nie je.

Príklad 1√1 - 4x x + 11.

Chcel by som, samozrejme, vyrovnať obe strany, aby som dostal kvadratická nerovnosť. V tomto prípade môžeme dostať nerovnosť, ktorá nie je ekvivalentná. Ak vezmeme do úvahy iba tie x, pre ktoré nie sú obe strany záporné (ľavá strana je zjavne nezáporná), potom bude kvadratúra stále možná. Ale čo robiť s tými x pre ktoré pravá časť negatívne? A nerobte nič, pretože žiadne z týchto x nebude riešením nerovnosti: koniec koncov, pre akékoľvek riešenie nerovnosti je pravá strana väčšia ako ľavá, čo je nezáporné číslo, a preto je samo sebou. nie negatívne. Takže dôsledkom našej nerovnosti bude takýto systém

1 - 4x (x + 11) 2

Tento systém však nemusí byť ekvivalentný pôvodnej nerovnosti. Oblasť definície výslednej sústavy je celá číselná os, pričom pôvodná nerovnosť je definovaná len pre tie x, pre ktoré je 1 - 4x ≥ 0. To znamená, že ak chceme, aby naša sústava bola ekvivalentná nerovnosti, musíme priradiť táto podmienka:

Odpoveď: (- 6; ¼]

Od silného študenta sa žiada, aby uvažoval všeobecný pohľad, dopadne to takto

√f(x) g (x) f (x) ( g(x)) 2

g(x) ≥ 0

f(x) ≥ 0.

Ak by pôvodná nerovnosť mala znamienko ≤ namiesto f (x) ≤ (g (x)) 2.

Príklad 2√x x - 2

Aj tu je možné odmocniť tie x, pre ktoré je splnená podmienka x - 2 ≥ 0, teraz však už nie je možné vyradiť tie x, pre ktoré je pravá strana záporná: koniec koncov, v tomto prípade je to tak. pravá strana bude menšia ako zjavne nezáporná ľavá strana, takže všetky takéto x budú riešeniami nerovností. Nie však všetky, ale tie, ktoré sú zahrnuté do rozsahu definície nerovnosti, t.j. pre ktoré x ≥ 0. Aké prípady treba zvážiť?

Prípad 1: ak x - 2 ≥ 0, potom naša nerovnosť implikuje systém

Prípad 2: ak x – 2

Pri analýze prípadov vzniká zložený stav nazývaný „totalita“. Získame množinu dvoch systémov ekvivalentných nerovnosti

Od silného študenta sa vyžaduje, aby zdôvodnil všeobecnú formu, potom to dopadne takto:

√f (x) g (x) f (x) (g (x)) 2

g(x) ≥ 0

f(x) ≥ 0

g(x).

Ak by pôvodná nerovnosť mala namiesto toho znamienko ≥, potom by sa f (x) ≥ (g (x)) 2 mala brať ako prvá nerovnosť tohto systému.

Príklad 3√x 2 - 1 √x + 5.

Aký význam majú výrazy vľavo a vpravo?

Dá sa to štvorčekovať?

Aký je rozsah definície nerovností?

Dostaneme x 2 - 1 x + 5

Ktorá podmienka je zbytočná?

Dostaneme teda, že táto nerovnosť je ekvivalentná systému

Od silného študenta sa vyžaduje, aby vykonal všeobecnú úvahu, ktorej výsledkom bude nasledovné:

√f (x) √g (x) f (x) g (x)

g(x) ≥ 0.

Zamyslite sa nad tým, čo sa zmení, ak namiesto pôvodnej nerovnosti bude znamienko ≥, ≤ resp

Na nástenke sú vyvesené 3 schémy riešení iracionálne nerovnosti, ešte raz sa rozoberá princíp ich konštrukcie.

4. fáza - upevnenie vedomostí (5 min.)

Žiaci skupiny 2 majú uviesť, ktorý systém alebo ich kombinácia je ekvivalentná nerovnosti č. 167 (Algebra a začiatky analýzy 10-11 ročníkov M, Vzdelávanie, 2005, Sh.A. Alimov)

Dvaja najpripravenejší študenti z tejto skupiny majú vyriešiť nerovnosti na tabuli: č. 1. √x 2 - 1 1

Č. 2. √25 - x 2

Študenti skupiny 1 dostanú podobnú úlohu, ale viac vysoký stupeň zložitosť č. 170 (Algebra a začiatky analýzy 10-11 ročníkov M, Vzdelanie, 2005, Sh.A. Alimov)

jeden z najpripravenejších študentov z tejto skupiny má vyriešiť nerovnosť na tabuli: √4x - x 2

Všetci študenti však môžu používať poznámky.

V tomto čase učiteľ pracuje so žiakmi v skupine 3: odpovedá na ich otázky a v prípade potreby pomáha; a riadi riešenie problémov na tabuli.

Po uplynutí času dostane každá skupina odpoveďový hárok na kontrolu (odpovede je možné zobraziť na obrazovke pomocou multimediálneho systému).

5. fáza hodiny – diskusia o riešeniach problémov prezentovaných na tabuli (7 min.)

Žiaci, ktorí plnili úlohy pri tabuli, svoje riešenia komentujú a ostatní v prípade potreby upravujú a robia si poznámky do zošitov.

6. fáza hodiny - zhrnutie hodiny, komentár k domácej úlohe (2 min.)

Skupina 3 si vymieňa karty v rámci skupiny.

2 skupina č. 168 (3, 4)

1 skupina č. 169 (5), č. 170 (6)