Szintézis rekurzív szűrők analóg prototípus alapján

Szabványos frekvenciaszelektív szűrők szintetizálása során célszerű egy jól fejlett berendezést használni az analóg szűrők számításához. A legtöbb széleskörű felhasználás a következő módszereket kapta:

1. Impulzusválasz invariancia módszer (standard transzformációs módszer).

2. Bilineáris transzformációs módszer.

3. A deriváltak véges különbségekkel való helyettesítésének módja.

4.2.1. Impulzusválasz invarianciás módszer (standard - transzformációs módszer)

Az impulzusválasz invarianciáján egy digitális szűrő impulzusválaszának mintáinak egyenlőségét értjük az analóg prototípus impulzusválaszának értékeivel, a mintavételi periódussal együtt.

A módszer megvalósításához szüksége van:

Keresse meg a prototípus impulzusválaszát;

Szerezze meg a digitális szűrő impulzusválaszát mintavétellel a léptékezési tényezőt figyelembe vevő periódussal:

; (4.1)

Keresse meg a szűrő átviteli függvényét úgy, hogy - a transzformációt - veszi :

. (4.2)

3.1 ábra – mintavételezés egy analóg prototípus impulzusválaszából

Tegyük fel, hogy az analóg prototípus átviteli függvénye egyszerű törtek összegeként van felírva:

. (4.3)

Ebben az esetben az inverz Laplace-transzformációnak megfelelően az analóg prototípus impulzusválasza a következő formájú:

. (4.4)

A mintavétel után megkapjuk a digitális szűrő szükséges impulzusválaszát:

A szintetizált digitális szűrő átviteli függvénye a transzformáció alkalmazása eredményeként a következő alakú:

Az így kapott átviteli függvény megfelel a digitális szűrő párhuzamos szerkezetének. Egy szintetizált digitális szűrő egyik linkjének blokkvázlata átviteli karakterisztikával a következő formájú: 3.2. ábra.

3.2 ábra – egy digitális szűrőszakasz blokkvázlata

Így a digitális szűrők impulzusválasz invariancia módszerrel történő szintetizálásának eljárása a következő lépéseket tartalmazza:

1. Állítsa be a digitális szűrő követelményeit.

3. Bontsd egyszerű törtekre!

4. Írja fel a digitális szűrő átviteli függvényét a (4.3) és (4.6) összefüggések alapján!

Az eredményül kapott szűrő frekvenciamenete az analóg prototípus frekvenciaválaszához ugyanúgy kapcsolódik, mint a mintavételezett jel spektruma az analóg jel spektrumához: periodikus ismétlés. Ezért megszerezni jó eredmények Ennél a módszernél az analóg prototípus erősítésének elhanyagolhatónak kell lennie a Nyquist-frekvencia feletti frekvenciákon. Ezért a módszer alkalmas aluláteresztő szűrők és PF-ek létrehozására, de nem alkalmazható felüláteresztő szűrők és RF szűrők fejlesztésére.

Példa az impulzusválasz invariancia módszer használatára

Legyen az analóg prototípus átviteli függvénye a következő:

.

Így a (4.3) kifejezésnek megfelelően az analóg prototípus alábbi paraméterei írhatók fel:

,

.

A (4.6) kifejezésnek megfelelően a következő kifejezést kapjuk a kívánt digitális szűrő átviteli függvényére:

.

Megkapjuk a digitális szűrési egyenletet. Ehhez a digitális szűrő átviteli függvényét a következő formában írjuk:

,

Ahol ,

.

Az utolsó kifejezés matematikai transzformációinak eredményeként a következőket kaphatjuk:

,

Miután a z-transzformációs képekről az eredetire váltunk, megkapjuk a digitális szűrési egyenletet:

4.2.2. Bilineáris transzformációs módszer

A Laplace-transzformáció és -transzformáció a következő relációval kapcsolódik egymáshoz:

. (4.7)

A (4.7) kifejezés nem használható közvetlenül az analóg prototípus ismert átviteli karakterisztikájával rendelkező digitális szűrő kiszámítására, mivel az inverz összefüggés transzcendentális:

. (4.8)

Ezt a nehézséget a sorozatbővítés segítségével lehet leküzdeni:

.

A bővítés első tagját felhasználva a következőket kaphatjuk:

. (4.9)

Ez a transzformáció az argumentum elsőrendű tört racionális függvénye, és ún bilineáris z – transzformáció.

A digitális szűrő átviteli függvénye az analóg prototípus átviteli függvényéből származik a következő helyettesítéssel:

. (4.10)

Tekintsük a bilineáris transzformáció tulajdonságait. Ehhez kapjuk:

. (4.11)

Így a bilineáris transzformáció az analóg prototípus frekvenciaválaszának jelentős deformációjához vezet, amikor digitális formába alakítják az eredeti arányhoz képest. . A prototípus frekvenciaválasz-frekvenciái és a digitális szűrő frekvenciái közötti összefüggést a következő összefüggés határozza meg:

.

Az analóg prototípus frekvenciája és a digitális szűrő frekvenciája közötti végső kapcsolat a következő:

. (4.12)

Az utolsó kifejezésnek megfelelően az analóg prototípus végtelen frekvenciaválasz tengelyének teljes tengelye teljesen a Nyquist intervallumban van a digitális frekvencia tengelyen 0-tól : 3.3. ábra. Következésképpen az impulzusválasz invariancia módszerében rejlő frekvenciajellemzők másolatainak szuperpozíciójának hatása teljesen kiküszöbölhető. Az alacsony frekvencia tartományban az analóg és digitális szűrők frekvenciakarakterisztikája megegyezik:

. (4.13)

3.3. ábra – A frekvenciatengely transzformációja bilineáris transzformáció során

Az utóbbi frekvenciacsatolási kifejezést használó áteresztősáv-határokkal jellemezhető frekvenciaszelektív szűrők esetében a frekvencia-válasz vetemítés hatása könnyen figyelembe vehető.

A szűrő kiszámításának folyamata a következő:

1) A számított szűrő frekvenciamenetét egy frekvenciaskálán állítjuk be, és ugyanabban a skálán jelöljük meg a frekvenciamenet jellemző pontjait.

2) Transzformációs függvény használata Az analóg prototípus frekvenciaskáláján ugyanazokat a jellemző pontokat határozzuk meg, és egy kifejezést állítunk össze az átviteli függvényéhez.

3) A bilineáris transzformációs módszerrel az átviteli függvényt egy digitális szűrő átviteli függvényévé alakítjuk.

Ezzel az analóg prototípus fázisválaszának deformációjával járó hátrányt kiküszöböltük.

A bilineáris transzformációs módszer teljesen kiküszöböli a frekvenciaválasz-aliasing hatását, és nem igényli a mintavételi frekvencia növelését a frekvenciaválasz-reprodukciós hibák csökkentése érdekében. A módszert akkor alkalmazzák, ha nincs szükség az analóg prototípus frekvenciaválaszának reprodukálásának nagyobb pontosságára.

Példa a bilineáris transzformációs módszer használatára

Leírjuk az analóg prototípus átviteli függvényét a következő kifejezéssel:

.

A (4.10) kifejezést figyelembe véve a következő kifejezést kaphatjuk a kívánt digitális szűrő átviteli függvényére:

,

Ahol ;

28 oldal (Word fájl)

Az összes oldal megtekintése

A mű szövegtöredéke

INFORMÁCIÓTECHNOLÓGIAI ÉS KOMMUNIKÁCIÓS MINISZTÉRIUM

SZÖVETSÉGI KOMMUNIKÁCIÓS ÜGYNÖKSÉG

KHABAROVSK INFOKOMMUNIKÁCIÓS INTÉZET

(ÁG) GOU VPO SZIBÉRIAI ÁLLAM

TÁVKÖZLÉSI ÉS INFORMÁCIÓTUDOMÁNYI EGYETEM

TANFOLYAM MUNKA

a digitális feldolgozás matematikai alapjairól

jeleket

Téma: Rekurzív digitális szűrő számítása

Különlegesség 210405

Rádiókommunikáció, rádióműsorszórás és televízió

30. számú lehetőség

Befejezve

Projekt menedzser

Fej Osztály

Habarovszk

	Műszaki feladat	3
	30. számú opció kiinduló adatai	4
	Bevezetés	5
1	A feladat grafikus ábrázolása	6
1.1	Rekurzív digitális szűrők tervezési módszerei	7
1.2	Numerikus integrációs módszerek	8
1.3	Impulzusválasz invariancia módszer	10
1.4	Bilineáris transzformációs módszer	12
1.5	Általánosított binomiális transzformáció	13
2.	Analóg szűrő átviteli függvényének kiszámítása és átalakítása digitális szűrő átviteli függvényévé	14
3.	Digitális szűrő blokkvázlata	22
4.	Digitális szűrő megvalósításának módszerei	23
4.1	Hardveres módszer	23
4.2	Szoftver módszer	24
4.3	Hardver-szoftver módszer	25
	Következtetés	27
	Bibliográfia	28

TECHNIKAI FELADAT

A kiindulási adatok alapján rekurzív digitális szűrőt kell kiszámítani.

A következő paraméterek tekinthetők meghatározottnak:

1 Szűrő típusa: aluláteresztő szűrő, aluláteresztő szűrő.

2 Szűrő típusa: Butterworth (B) vagy Chebyshev (C).

3 Mintavételi frekvencia fd.

4 sávszélesség-korlát (PB):

Az aluláteresztő szűrő fп áteresztősávjának felső határa;

A felüláteresztő szűrő fп áteresztősávjának alsó határa;

5 A feltartóztatási sávok határai (DP);

PV fz alsó határa aluláteresztő szűrőhöz;

A PV fz felső határa a felüláteresztő szűrőhöz.

6 Az amplitúdó-frekvencia válasz megengedett egyenetlensége a PP-ben ∆A max, dB.

7 Minimális megengedett csillapítás PZ A min-ben, dB.

KIINDULÓ ADATOK A 30. OPCIÓHOZ

Aluláteresztő szűrő típusa

Butterworth szűrő típus

Mintavételi frekvencia fd = 16 kHz

Sávszélesség korlátok fп = 1,7 kHz

Stopsáv határértékei fз = 3,8 kHz

Megengedett PP egyenetlenség ∆A max = 1,35 dB

A szabad zóna megengedett csillapítása A min = 25 dB.

Tanár___________ Diák_______ ____________

„__27__” _______2011. május_______

BEVEZETÉS

A jó minőségű frekvenciájú, nem rekurzív digitális szűrők (NCF) általában nagy ablakszélességgel rendelkeznek (polinomiális szűrőoperátor). Minél kisebb a szűrő frekvenciaválaszának átmeneti zónájának megengedett szélessége az áteresztő és elnyomó sávok között, annál nagyobb a szűrőablak. Alternatív megoldás a rekurzív digitális szűrők (RDF) alkalmazása, amelyeknél az NDF-hez képest több nagyságrenddel csökkenthető a szűrési együtthatók száma.

A rekurzív szűrőknek van egy bizonyos „memóriája” a korábbi minták értékei alapján, amely határon belül végtelen lehet. Ezt a tényezőt figyelembe véve a rekurzív szűrőket végtelen impulzusválasz szűrőknek (IIR szűrőknek) nevezik, ellentétben a nem rekurzív szűrőkkel, amelyeknek mindig véges impulzusválasza van (FIR szűrők). A rekurzív szűrő jelre adott válasza a „memória” figyelembevételével kiküszöböli az egyenletes impulzusválaszú szűrők létrehozásának lehetőségét, és a rekurzív szűrők frekvenciakarakterisztikája mindig összetett. Adott frekvenciakarakterisztikával rendelkező rekurzív frekvenciaszűrők tervezése z-transzformációk segítségével történik.

1. A probléma grafikus ábrázolása

Jelenítsük meg grafikusan az aluláteresztő szűrő frekvenciaválaszára vonatkozó követelményeket, ehhez ki kell számítani:

1. ábra – A Butterworth szűrő frekvenciaválasza és a szűrő frekvenciaválasza

Butterworth a Db-ben.

1.1. Rekurzív digitális szűrők tervezési módszerei

A digitális IIR szűrők átviteli függvényét az összefüggés adja meg , amely hasonló az AF átviteli funkcióhoz, amikor a z változót s-re cseréljük. Ezért a digitális IIR szűrők tervezésének egyik megközelítése az AF átviteli függvény DF átviteli funkcióvá alakítása. Ahhoz, hogy a CF-ek a szükséges tulajdonságokkal rendelkezzenek AF-ként, két feltételnek kell teljesülnie:

1. Az s-sík képzeletbeli tengelyét () a z-síkban egységkörré képeztük le ( ). Ez a feltétel szükséges az AF frekvencia jellemzőinek megőrzéséhez.

2. Az s-sík () bal fele a z-síkban az egységkör () belsejében jelent meg. Ez a feltétel szükséges az AF stabilitási tulajdonságainak megőrzéséhez.

1.2. Numerikus integrációs módszer

Az AF-et leíró differenciálegyenletet a CF differenciálegyenlet váltja fel, a deriváltot néhány véges különbséggel közelítve. Ez a művelet az AF átviteli függvény s összetett változójának a CF átviteli függvény z összetett változójával való helyettesítéséhez vezet.

Különféle numerikus integrációs módszerek adják meg különféle funkciókatátmenetet, és ebből következően a különböző digitális funkciókat. Tekintsük az Euler-féle módszert, amely közelíti az idő deriváltját folyamatos funkció a forma véges különbsége

, ahol T a mintavételi intervallum, és y(n)=y(nT). Operátoros formában az egyenlet megadja

.

Mutassuk meg ez a módszer megfelel a fenti két feltételnek:

1. vagy ebből következik, hogy nál nél .

Önkormányzati költségvetési oktatási intézmény tornaterme 9. sz

KÍSÉRLETI-ABSZTRAKT PROJEKT

ebben a témában:

Az invariánsok módszerének alkalmazása egységes államvizsga- és olimpiai feladatok megoldásában

Teljesített:

tanítvány XI"B" osztály

Tiscsenko Elina

Tudományos igazgató:

matematika tanár

Khatuntseva

Irina Vladimirovna

Voronyezs – 2017

Tartalom

Bevezetés

A modern matematikában fontos szerepet játszik az invariancia fogalma, i.e. egy matematikai objektum megváltoztathatatlansága. A matematika számos meghatározása valójában ehhez a fogalomhoz kapcsolódik, bár maga az invariancia kifejezés hiányzik a tankönyvekből.

Példa: páros funkció Az R definíciós tartományú f(x) invariáns, mert f(x)= f(-x).

Az invariancia egyik vagy másik tulajdonságának jelenléte egy matematikai objektumban lehetővé teszi, hogy megállapítsuk ennek az objektumnak néhány általános minőségi tulajdonságát.

A munka célja, hogy bemutassa az invariáns módszer alkalmazását az egységes államvizsga- és olimpiai feladatok megoldásában.

Az ország vezető egyetemeinek, például a Moszkvai Állami Egyetemnek és a Moszkvai Fizikai és Technológiai Intézetnek sok irodalma foglalkozik ezzel a témával. Az invariánsok elméletének klasszikus könyve a kiváló német matematikus, Herlean Weyl könyve. Az Oxfordi Egyetem hallgatói pedig évente adják ki a „The Invariant” című magazint.

Ez a téma nagyon aktuálisnak tűnik, mert... Az invariáns módszer lehetővé teszi a problémák egyszerű megoldását magasabb szint nehézségek.

1. fejezet Az invarianto módszer alkalmazása olimpiai feladatok megoldásában

A paritást (páratlan paritást), az osztás maradékát, a permutációt, a színezést stb. leggyakrabban invariánsnak tekintik.

A paritás használata az egyik leggyakrabban előforduló ötlet az olimpiai feladatok megoldása során. Fogalmazzuk meg a legfontosabb állításokat, amelyekre ennek az elképzelésnek az alkalmazása alapszik:

több egész szám összegének paritása egybeesik a páratlan tagok számának paritásával;

több (nullatól eltérő) szám szorzatának előjelét a negatív tényezők számának paritása határozza meg.

1. feladat.

Tíz pro és tizenöt kontra van felírva a táblára. Bármely két karakter törölhető, és helyette pluszt írhat, ha megegyezik, és mínuszt egyébként. Milyen jel marad a táblán huszonnégy ilyen művelet elvégzése után?

Megoldás.

Cserélje ki minden pluszt egy számra1 , és minden mínusz egy szám-1 .

Ezután tetszőleges két számot törölünk, és felírjuk a szorzatát. Ezért a táblára írt összes szám szorzata változatlan marad.

Mivel a termék kezdetben negatív volt (15 negatív számok), akkor a végén megmaradnegatív.

Válasz: mínusz.

2. feladat.

A fiú rossz jegyet kapott egy matematikai vizsgán, és kétségbeesésében tíz darabra tépte a papírt a munkájával. Aztán az egyik így kapott darabot további 10 darabra tépte. Lehet-e 2015-ös papír a lazítás végén?

Megoldás.

Minden alkalommal, amikor 10-zel eltép egy papírt, a fiú 9-el növeli az összes papírdarab számát. Az első tépés után 1+9=10 darab lesz, a második után - 10+9=19 darab stb. . Vagyis a papírdarabok számát az n-edik szakadásnál az 1+9 képlet határozza megn.

Vizsgáljuk meg, hogy a 2015-ös szám 1+9-ként ábrázolható-en:

1+9 n=2015;

9 n=2014.

2014 nem osztható 9-cel maradék nélkül, ezért nem lehet 2015 darab a relaxáció végén.

Válasz: Nem

3. feladat.

A tábla 1-től 1998-ig terjedő számokat tartalmaz. Egy mozdulattal tetszőleges két számot törölhet, és helyette felírhatja a különbséget, amíg egy szám nem marad. Lehet, hogy ez a szám nulla?

Megoldás.

Tekintsük a táblára egy lépés előtt és után felírt összes szám összegét. Törölhetjük a számokata, b. Ekkor először az összes szám összege egyenlő volt , majd holS– az összes többi szám összege. Amint látjuk, a csere (a+ b) tovább (a- b) nem változtatja meg az összes szám összegének paritását. A legelején lévő számok összege egy páratlan szám (
), ami azt jelenti, hogy minden lépésben a táblára írt számok összege páratlan lesz. A nulla páros szám, ezért nem tudjuk feltenni a táblára.

Válasz: nem.

4. feladat.

Egy 2*2 négyzet alakú asztal minden cellája feketére van festve, ill fehér szín, ahogy az alábbi ábrán is látható. Egy mozdulattal átszínezheti a cellákat bármelyik sorban, bármelyik oszlopban vagy bármilyen átlóban: feketéket - fehéreket és fehéreket - feketét. Lehetséges néhány mozdulattal olyan asztalt kapni, ahol minden cella fehér?

Megoldás.

Adjunk minden cellához 1-et, ha fehérre festették, és -1-et, ha feketére festették. Ekkor a színek megváltoztatása a jelek megváltoztatását jelenti. Tekintsük a celláknak megfelelő összes szám szorzatát. Mivel az átszínezés során pontosan két tényező előjelét változtatjuk meg, mind a négy szám szorzata nem változik. Kezdetben ez a szorzat egyenlő -1. A szükséges színezés 1-gyel egyenlő terméknek felel meg. Ezért lehetetlen a táblázatot a jelzett műveletekkel újraszínezni.

Válasz: nem.

5. feladat.

Három kupac 1, 9 és 98 követ tartalmaz. Egy mozdulattal bármelyik két kupacból kivehet egy követ, és áthelyezheti a harmadikba. Lehetséges néhány mozdulattal összeszedni az összes követ az egyik kupacban?

Megoldás.

Vegyük figyelembe a maradékokat, amikor az eredeti számokat hárommal osztjuk - a halomban lévő kövek számával. Az első halomban a maradék 1, a másodikban - 0, a harmadikban - 2. Nézzük meg, mi történik ezután a maradékok szempontjából, amikor eltoljuk a köveket:

Találtunk egy invariánst - bármelyik művelet után a maradékok ugyanazok lesznek: 0, 1, 2, csak másképp oszlanak el. Ha össze tudjuk gyűjteni az összes követ egy kupacba, akkor a maradék 3-mal elosztva minden halomban azonos lesz (0-val egyenlő). Következésképpen lehetetlen az összes követ egy halomba gyűjteni a jelzett műveletekkel.

Válasz: nem.

6. feladat.

A síkon adott egy nem önmagát metsző zárt szaggatott vonal, amelynek nincs három csúcsa ugyanazon az egyenesen. Nevezzünk egy pár nem szomszédos hivatkozást vonalláncnakkülönleges, ha az egyik folytatása metszi a másikat. Bizonyítsuk be, hogy a speciális párok száma páros.

Megoldás.

Vegyük a szomszédos AB és BC linkeket, és hívjuk meg őketsarok a B ponthoz viszonyított ABC szögre szimmetrikus szög (az alábbi ábrán a sarok árnyékolt). Ugyanazok a sarkok figyelembe vehetőek a szaggatott vonal összes csúcsánál. Nyilvánvaló, hogy a speciális párok száma megegyezik a linkek és a sarkok metszéspontjainak számával. Meg kell jegyeznünk, hogy az egyik sarokkal metsző szaggatott vonal szakaszainak száma páros, hiszen az A-ból C-be menet a szaggatott vonal annyiszor lép be a sarokba, ahányszor elhagyja azt (ez abból a feltételből következik, hogy a szaggatott vonal három csúcsa nem esik ugyanazon az egyenesen). Ezért a speciális párok száma páros, amit bizonyítanunk kellett.

7. feladat (az iskolások összoroszországi olimpiájának regionális szakasza, 2016-2017, 11. osztály, második nap, 8. szám).

Kezdetben 100 kártya kerül az asztalra, mindegyikre egy-egy természetes szám van írva; Sőt, köztük pontosan 28 páratlan számú kártya van. Ezután a következő eljárást percenként hajtják végre. Minden 12 asztalon heverő kártyához kiszámolják a ráírt számok szorzatát, ezeket a szorzatokat összeadják, és a kapott számot egy új kártyára írják, amelyet az asztalon heverőkhöz adnak. Meg lehet-e választani a kezdeti 100 számot úgy, hogy bármely természetes d-re előbb-utóbb egy olyan kártya legyen, amelynek a szám osztható
?

Megoldás.

Ha egy pillanatban pontosan k páratlan szám van a kártyákon lévő számok között, akkor a számok szorzatai között pontosan 12
páratlan; ezért a következő hozzáadott kártyán lévő szám pontosan akkor lesz páratlan, amikor páratlan (és ekkor k 1-gyel nő abban a percben).

Könnyen belátható, hogy a szám
páratlan (ez abból a tényből következik, hogy a kettő hatványait tartalmazza
És
, egyenlőek). Továbbá a szekvenciális ellenőrzés során azt találjuk, hogy az első
,
,
- páratlan számok, és
- még. Ezért, ha a páratlan kártyák száma eléri a 32-t, nem fog tovább növekedni, és mindig csak 32 páratlan kártya lesz az asztalon, és minden hozzáadott szám páros lesz.

Hagyja most n-következő lépés – a kártyákra írt számok 12 szorzatának összessége, és – 11 szám összes szorzatának összege. Szám
, amely a következő kártyára lesz írva, eltér a 12 szám szorzatának összegére, amelyek között van egy most összeadott páros szám , azaz tovább
. Azt jelenti,. Szám - páros, mivel a páratlan összegek száma 11
még. Eszközök,
páratlan, és kettő maximális hatványa, amely osztható vele
egyenlő kettő maximális hatványával, amely osztható . Ez azt jelenti, hogy mivel kezdetben nem voltak számok az asztalon, ami bármilyen természetesdosztották -vel, akkor ezek a számok nem jelennek meg tovább.

Válasz: nem, nem lehet.

2. fejezet Az invariánsok módszerének alkalmazása paramétert tartalmazó Unified State Examination feladatokban

Elemzés után nagy mennyiség problémák megoldására algoritmust állítottunk össze egy paraméterrel az invariánsok módszerével történő problémák megoldására.

Algoritmus a paraméterekkel kapcsolatos problémák megoldására invariáns használatával:

1) ellenőrizze a változatlanságot adott egyenlet, egyenlőtlenség, egyenletrendszer (egyenlőtlenségek);

2) megtalálni érvényes értékek paraméter a feltételek teljesülésének ellenőrzéséből: a „szimmetria a változó előjeléhez képest” helyett annak nulla értékét; a „szimmetria a változók permutációjára vonatkozóan” minden változót egy betűvel jelölünk;

3) ellenőrizze, hogy a talált paraméterértékek megfelelnek-e a probléma feltételeinek;

4) írja le a választ.

1. állítás . Ha a kifejezés
invariáns alatt átalakítás
és egyenlet
gyökere van ,Hogy

2. állítás. Ha a kifejezés

és egyenlet
van megoldása
, majd egy számpár

3. állítás . Ha a kifejezés
transzformációs invariáns
és egyenlet
van megoldása
, majd egy számpár
ennek az egyenletnek a megoldása is.

4. állítás. Ha a kifejezés
transzformációs invariáns
És
, és az egyenlet
van megoldása
, aztán pár szám
ennek az egyenletnek a megoldása is.

5. állítás. Ha a kifejezés
transzformációs invariáns
, az egyenlet
gyökere van , Hogy
ennek az egyenletnek a gyökere is.

1. feladat.

Keresse meg az a paraméter összes értékét, amelyre az egyenletnek egy megoldása van

Megoldás.

Vegye figyelembe, hogy ha az egyenlet gyöke, akkor - - gyök is => csak akkor lehet egy gyök, ha =-=0.
Cseréljük
:

Nál nél
:

1 gyökér, alkalmas

Nál nél
:

Bal oldal ez az egyenlet nagyobb vagy egyenlő
, és ez az alsó határ pontos - eléri a
. A jobb oldal becslése kicsit nehezebb. Először is vegye figyelembe, hogy változó megváltoztatásakor tól től
előtt
kifejezés
-1-ről 1-re változik. A szegmensen
funkció
től monoton növekszik
előtt
. Ezért a kifejezés
től változik
előtt
. Ennek megfelelően az (1) egyenlet jobb oldala innen változik
előtt
, és az egyenlet jobb oldalának értékei teljesen kitöltik ezt a szegmenst. A vonatkozó információkból lehetséges értékek balra és megfelelő részek Az (1) egyenletből az következik, hogy csak akkor lehetnek egyenlőek, ha egyidejűleg egyenlőek
. Más szavakkal, az (1) egyenlet ekvivalens a rendszerrel:

Az első egyenletnek egyetlen gyöke van
, ami a rendszer második egyenletét is kielégíti. Ez azt jelenti, hogy a rendszernek és vele együtt az eredeti egyenletnek is van egyetlen döntés
. Ezért a paraméter ellenőrzött értéke (
) szerepelnie kell a feladatválaszban.

Válasz: 0;
.

2. feladat. egyenlőtlenségek rendszere
van egyetlen megoldás?

Megoldás. 1. Ebben a rendszerben megfigyeljük a „szimmetriát a változók változása tekintetében”. Akkor, ha van megoldás a rendszerre, akkor
a rendszer megoldása is. A megoldás egyedisége a feltételek mellett érhető el
(4. állítás).

2. Az összes változó kijelölése a
Egy olyan egyenlőtlenségből, amelynek egyedi megoldása van, ha a diszkrimináns másodfokú trinomikus egyenlő nullával, azok.

3. Ellenőrizzük, hogy a rendszer rendelkezik-e egyedi megoldással a talált paraméterértékekre.

a) Cseréljük be ezt a rendszert egyenlőtlenségek
:

Adjuk össze az utolsó rendszer egyenlőtlenségeit:
+

A zárójeleket kinyitva és hasonló kifejezéseket hozva a következőket kapjuk: . Innen



- csak döntés.

b) Csere után
mi kapjuk az egyetlen megoldást

Válasz:

3. feladat. Keresse meg annak a paraméternek az összes értékét, amelyre az egyenletrendszer

négy különböző megoldással rendelkezik.

Megoldás.

A rendszer formájából az következik, hogy > 0.

1. A rendszer invariáns, ha helyére - és tovább - . Ezért ha a kívánt paraméterértéket és egy számpárt ;
- a rendszer megoldása, majd párok
;
, ;
És
; -
rendszermegoldások is. (2. és 3. állítás). Ezért megoldásokat találunk nál nél ≥ 0, ≥0. Ábrázoljuk az egyenletek grafikonjait egy koordinátarendszerben. Az első egyenlet grafikonja - a négyzet oldalainak pontjaiABCD, a második grafikonja egy kör, amelynek középpontja az origóban van, sugara pedig egyenlő.

Az ábrán látható, hogy a rendszernek pontosan négy megoldása van két esetben: 1)


;
; mert > 0, akkor
; 2) = 0 E- egy olyan négyzetbe írt kör sugara, amelynek oldala egyenlő
Pythagoras szerint a BOS háromszögből.

Eszközök, 0E =
, akkor =
ahol 2
= 2; 2 =
és =
.

Válasz: = 1; =
.

4. feladat. Milyen paraméterértékeken egyenletrendszer
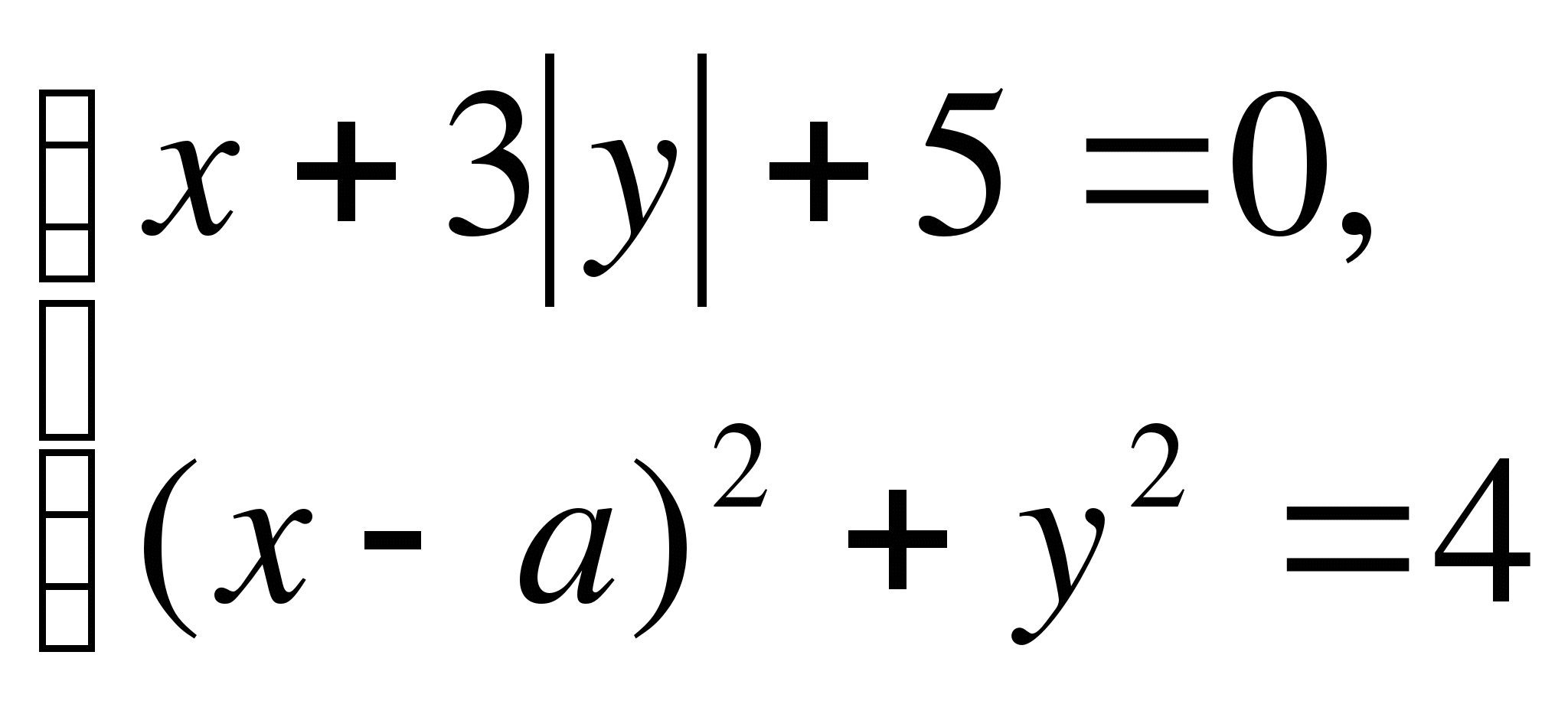pontosan három megoldása van?

Megoldás. 1. Ha egy számpár ;
– a rendszer megoldása, - a kívánt paraméter, majd a pár

; -
– megoldás is a rendszerre. Eszközök, = -
= 0.(3. állítás).

2. Cseréljük = 0 ebbe az egyenletrendszerbe.

Kapunk:

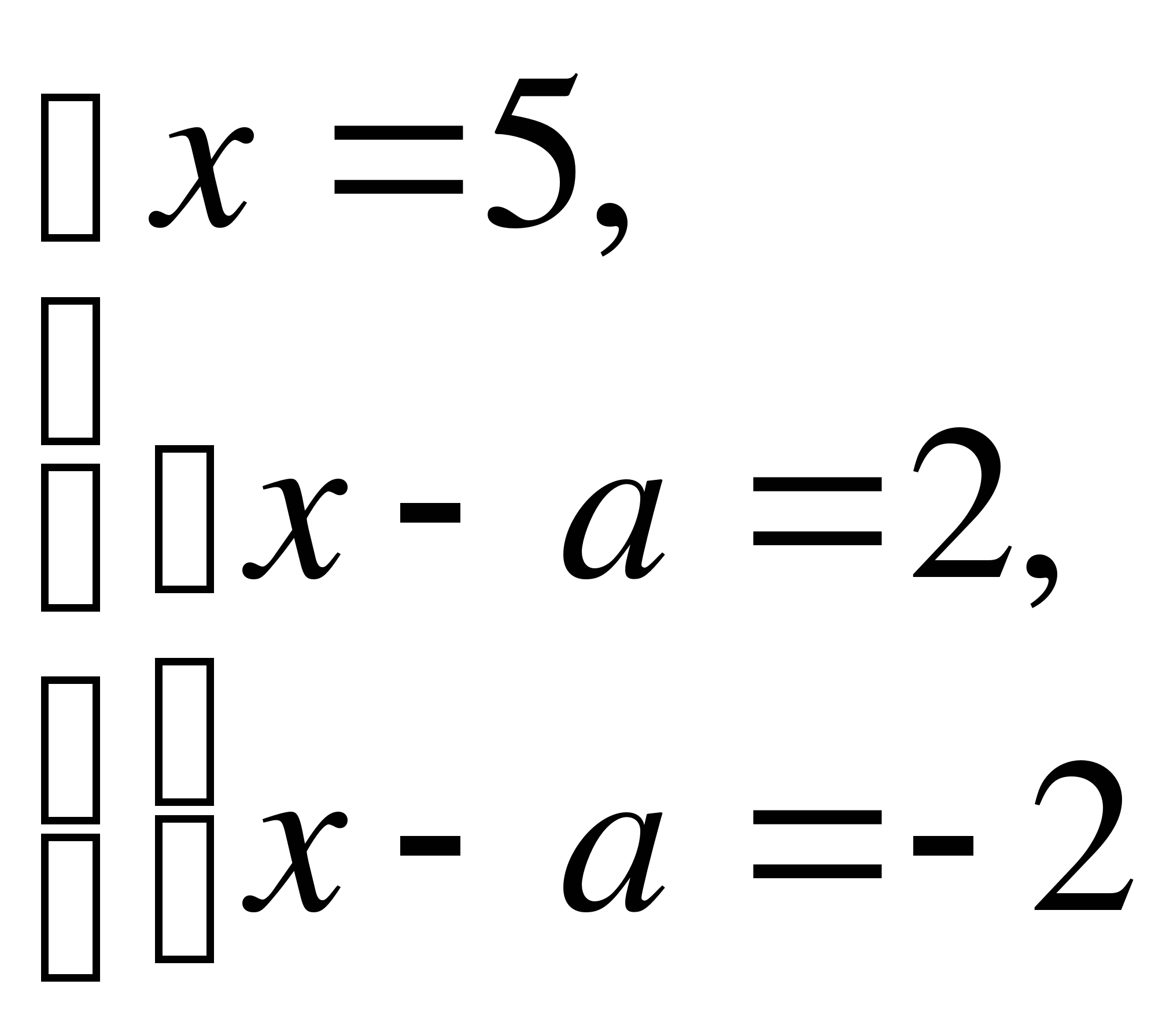
Nézzük meg, hogy van-e ez az egyenlet a talált értékekkel egyetlen döntés. Nál nél =-3 van:

Oldjuk meg a rendszer második egyenletét:

vagy
nincsenek megoldásai.

Ha y=0, akkor x=5 és (-5; 0) a rendszer egyetlen megoldása. Eszközök,
nem illik.. Következtetés

Az elvégzett munka során az invariánsok módszerét tanulmányoztam. Az invariánsok módszere a paramétert tartalmazó egységes államvizsga-feladatok és a színezési, paritási, osztási maradékokra vonatkozó olimpiai feladatok megoldására szolgált, indokolt és jól látható módon. gyakorlati használat módszer.

Felhasznált irodalom jegyzéke

INVARIÁNS MÓDSZER MATEMATIKAI FELADATOK MEGOLDÁSÁRA

Ostonov K.

(Szamarkand Állami Egyetem)

Egyes matematikai feladatok megoldása során a kívánt objektum transzformációinak halmazát használjuk, és ezeknek a transzformációknak a segítségével egy másikat kell előállítani az objektum egyik állapotából. A lehetőségek felsorolásával sok esetben ellenőrizhető a „nem” válasz érvényessége, de a kapott eredmény helyességének bizonyítása nehéz lesz. Az invariáns módszer az ilyen problémák megoldásának ilyen matematikai módszere. Először is definiáljuk, mi az invariáns?

1. definíció. Az invariáns az, ami nem változik az átalakítások során.

Például egy invariáns lehet egy szám, egy számhalmaz, egy szám paritása stb.

1. tulajdonság. Ha egy objektum két állapotában egy invariáns értéke eltérő, akkor az egyiket a másikból nem lehet megszerezni.

Számos matematikai feladatban a számok páratlansága (páratlansága) és az osztás maradéka invariánsnak számít.

Itt mindenekelőtt a páros és páratlan szám definícióján, a paritás absztrakt fogalmán, a „különböző paritású” számokon, valamint azon a tulajdonságon alapul, hogy egy összeadásakor a számok paritása megváltozik. A páros és páratlan elv használatához a következő állítások alkalmazása szükséges:

1. állítás. Több egész szám összegének paritása egybeesik a páratlan tagok számának paritásával.

Nyilatkozat2. Több (nem 0) szám szorzatának előjelét a negatív tényezők számának paritása határozza meg.

1. feladat. A 11-es számot felírják egy papírra. Lehet, hogy az eredmény a 0?

Megoldás. Megkérjük a tanulókat, hogy hajtsák végre ezt a műveletet (minden lépés eredménye fel van írva a táblára), fel kell jegyezni egy mintát: minden lépés után megváltozik a paritás jellege: az első tanuló után a szám páros, a második után páratlan lesz. ; a harmadik után - páros; a negyedik után – páratlan. Aztán a tizenhatodik után a szám páratlan lesz. Ezért nem lehet nulla a végén.

2. feladat. Egy fogason 20 sál lóg. 17 lány felváltva megy a fogashoz, és leveszi vagy felakasztja a sálat. Maradhat pontosan 10 sál a lányok távozása után?

Megoldás. Az első lány közeledtével a megmaradt sálak száma vagy 19 vagy 21 (páratlan szám); miután a második lány közeledik - vagy 18, vagy 20, vagy 22 (páros szám); miután a harmadik lány közeledik - vagy 17, vagy 21, vagy 23, vagy 19 (páratlan szám). A 17. lány közeledtével páratlan számú sál marad. Kiderül, hogy ez ellentmondás. Ez azt jelenti, hogy nem maradhat 10 sál.

3. feladat. Egy olyan táblázatban, ahol 15 szám (-1) van, a következő műveletet hajthatja végre: egyszerre változtassa meg két (nem több, nem kevesebb) szám előjelét a táblázatban. Elõállítható-e ennek a mûveletnek véges számú végrehajtásával egy (+ 1)-bõl álló táblázat?

Megoldás. Válasz: nem. Mivel a táblázatban szereplő számok száma páratlan, és minden művelet után a táblázatban szereplő számok száma (+ 1) páros. Az invariánsok nyelvén ez azt jelenti: a táblázat invariánsa a beírt művelethez képest a táblázatban szereplő összes szám szorzata. A kezdeti pillanatban ez a szorzat egyenlő (- 1), és olyan táblázatot kell kapnunk, amelynek invariánsa egyenlő (+ 1).

4. feladat. Van egy számkészlet. Ez a számkészlet számok hármasára változik:
,
,
. Adott egy 2016, 2018, 2019 számhalmaz. Lehet belőle 2017, 2018, 2019 számhalmazt kapni?

Megoldás. Válasz: nem. Mert
És
+
+
egyenlőek, de a 2016+ 2018+ 2019 és a 2017+ 2018+ 2019 összege eltérő.

5. feladat. A 2, 3, 4,... 9 számokból két természetes szám készült. Minden számjegyet egyszer használtak. Lehet, hogy az egyik szám kétszerese a másiknak?

Megoldás. Válasz: nem. Hadd És
– a kapott számok, S( a) és S( b) – számjegyeik összege. Az oszthatósági teszt szerint az N és S(N) számoknak 3-mal osztva ugyanazok a maradékai. Mivel a szám a+b = 3a osztható 3-mal, akkor az S = S( a) + S( b) osztható 3-mal, ami helytelen, mivel S = 2 + 3 + 4 + … + 9 = 44.

6. feladat. A 0, 1, 2, 3, …, 9 számokat körbe írjuk. Egy lépésben ugyanazt az egész számot hozzáadhatja két szomszédos számhoz. Lehetséges néhány mozdulattal tíz nullát kapni?

Megoldás. Ez tiltott. Ha a megadottak közül bármelyik kettőhöz azonos egészeket adunk, az nem változtatja meg az összes szám összegének paritását. Kezdetben ez az összeg 1 + 2 + 3 + … 9 = 45, ezért minden lépés után a kapott számok összegének páratlannak, a nullának pedig párosnak kell lennie.

7. feladat. Tíz edényben 1, 2, 3,..., 10 liter víz van. Az A edényből a B edénybe annyi vizet szabad önteni, amennyi a B edényben van. El lehet érni, hogy többszöri transzfúzió után 5 edényben 3 liter, a maradékban 6, 7, 8, 9, 10 legyen? azok?

Megoldás. Ez tiltott. A javasolt művelet félig invariáns: bármilyen transzfúzió esetén a páratlan edények száma (amelyek páratlan számú liter vizet tartalmaznak) nem növekszik. Az ilyen erek száma csökken, ha páratlan számú edényből páratlan számú edénybe transzfundálják, más esetekben pedig nem változik. Ezért az 1, 2, ... 10 - 3, 3, 3, 3, 3, 6, ..., 10 átmenet lehetetlen, mivel növeli a páratlan erek számát.

A páros és páratlan számokat használó rejtvényfeladatok megoldásait a logikai kifogástalanság és a következtetések abszolút érvényessége különbözteti meg, amelyekhez szükség van az összeadás és kivonás aritmetikai műveleteinek legegyszerűbb tulajdonságainak ismeretére.

Itt a következő alapvető paritási szabályok érvényesek:

A páros tagok összege páros.

Ha a páratlan tagok száma páros, akkor az összeg páros.

Ha két szám összege páros szám, akkor a különbségük is páros szám.

Ha két szám összege páratlan szám, akkor a különbségük is páratlan szám.

Ha a páratlan tagok száma páratlan, akkor az összeg páratlan.

Ha az egyik tényező páros szám, akkor a szorzat páros.

Ha minden tényező páratlan, akkor a szorzat páratlan.

8. probléma. Az 1+2+3+4+…+2000 szám páros vagy páratlan? Válasz: egyenletes.

9. feladat. Igaz-e az 1x2+2x3+3x4+…+99x100 = 20002007 egyenlőség? Válasz: nem, a páros tagok összege mindig páros.

10. probléma. .Határozzuk meg a 3(x+1) szám paritását; x+x; x+x+2005, ha x páratlan. Válasz: az első páros, a második páros, a harmadik páratlan.

11. probléma. Vágható-e egy 25x25-ös négyzet 1x2-es téglalapokra? Válasz: nem, a 625-ös szám nem osztható 2-vel.

12. probléma. Össze lehet kötni 13 várost utakkal úgy, hogy minden városból pontosan 5 út vezet ki? Válasz: nem, minden utat kétszer számolunk, tehát az összes utak számának párosnak kell lennie. A mi esetünkben 13x5 = 65 van.

13. probléma. A szöcske egyenesen ugrik: először 1 cm-t, másodszor 2 cm-t stb. 25 ugrás után visszatérhet az előző helyére? Válasz: nem, a régi helyre való visszatéréshez a centiméterek összszámának párosnak kell lennie, az 1+2+3+...+25 összegnek pedig páratlannak kell lennie.

14. probléma. Lehet-e olyan sakkversenyt rendezni 15 sakkozó között, hogy minden játékos 15 partit játsszon? Válasz: nem, a 15x15 páratlan.

15. probléma. Lehet-e három egymást követő összeg szorzata természetes számok a következő három természetes szám összege 33333? Válasz: nem, a terméknek egyenletesnek kell lennie, mert az egyik tényező a páros szám.

Összefoglalva azt mondhatjuk, hogy a páros és páratlan ötlet használata lehetővé teszi a diákok számára cáfolja meg azokat a tényeket, amelyekről kérdez, és értse meg az ellentmondásos bizonyítási módszerhez hasonló logikát. A leggyakrabban előforduló „nem” válasz mellett pontosan meg kell magyarázni, hogy ez miért nem fordulhat elő. Ha azt mondja: „Talán”, akkor elegendő példát adni egy ilyen elrendezésre, elosztásra vagy kombinációra. Az egyenlőség és a páratlanság közvetlen problémái mellett magában foglalhatja a koncepcióban hasonló (két ellentétes) problémák elemzését is, amelyeket egy objektum (vagy opció) egyik vagy másik csoporthoz való hozzárendelésének elemzésével oldanak meg.

Irodalom

Alkhova Z. N., Makeeva A. V. Tanórán kívüli tevékenységek matematika. – Szaratov: „Líceum”, 2001.

Vilenkin N. Ya. Népszerű kombinatorika. - M.: Oktatás, 2003.

Kozlova E. G. Mesék és tippek (matematikai kör feladatai). 2. kiadás, rev. és további – M.: MTsNMO, 2004.

4. Mednikov L.E. Parity.-M.: MTsNMO, 2009.

5. Babich O.A. A tanórán kívüli matematika óra forgatókönyve (7. évfolyamon belül, Kholmsk, 2015).

6. www.strategy48.ru/sites/default/files/fomina1.pdf

annotáció

Ez a cikk a matematikai problémák megoldásának egyik módszerét tárgyalja - az invariáns módszert, amely a páros és páratlan elképzelésen alapul, valamint azok sajátosságait, amikor szórakoztató feladatokat oldanak meg egy iskolai matematika tanfolyamon.

Kulcsszavak : invariáns, feladat, ötlet, paritás, szám, szabályok, minta.