Gauss-módszer, hogyan kell részletesen megoldani. Gauss módszer: lineáris egyenletrendszer megoldási algoritmusának leírása, példák, megoldások

A Gauss-módszer, amelyet az ismeretlenek szekvenciális kiküszöbölésének módszerének is neveznek, a következő. Elemi transzformációkkal egy lineáris egyenletrendszert olyan formára hozunk, hogy az együttható mátrixa trapéz alakú (ugyanúgy, mint a háromszög vagy lépcsős) vagy közel trapéz alakú (közvetlen löket a Gauss-módszer, a továbbiakban - egyszerűen egyenes löket). Példa egy ilyen rendszerre és megoldására a fenti ábrán.

Egy ilyen rendszerben az utolsó egyenlet csak egy változót tartalmaz, és annak értéke egyértelműen megtalálható. Ennek a változónak az értéke ezután behelyettesítésre kerül az előző egyenletbe ( fordított löket Gauss módszer , akkor csak fordítva), amelyből az előző változó található, és így tovább.

Egy trapéz (háromszög alakú) rendszerben, mint látjuk, a harmadik egyenlet már nem tartalmaz változókat yÉs x, és a második egyenlet a változó x .

Miután a rendszer mátrixa trapéz alakot öltött, már nem nehéz megérteni a rendszer kompatibilitásának kérdését, meghatározni a megoldások számát és maguknak megtalálni a megoldásokat.

A módszer előnyei:

rendszerek megoldása során lineáris egyenletek a háromnál nagyobb egyenletek és ismeretlenek számával a Gauss-módszer nem olyan nehézkes, mint a Cramer-módszer, mivel a Gauss-módszerrel való megoldás kevesebb számítást igényel;
a Gauss-módszerrel határozatlan lineáris egyenletrendszerek is megoldhatók, azaz van egy általános megoldás (és ezeket ebben a leckében elemezzük), a Cramer-módszerrel pedig csak azt állíthatjuk, hogy a rendszer határozatlan;
meg tud oldani olyan lineáris egyenletrendszereket, amelyekben az ismeretlenek száma nem egyenlő az egyenletek számával (ebben a leckében ezeket is elemezzük);
A módszer elemi (iskolai) módszereken alapul - az ismeretlenek helyettesítésének módszerén és az egyenletek összeadásának módszerén, amelyeket a megfelelő cikkben érintettünk.

Annak érdekében, hogy mindenki megértse, milyen egyszerűséggel oldják meg a trapéz alakú (háromszög alakú, lépcsős) lineáris egyenletrendszereket, bemutatunk egy ilyen rendszerre fordított mozgást alkalmazó megoldást. Ennek a rendszernek a gyors megoldását az óra elején lévő képen mutattuk be.

1. példa Oldjon meg egy lineáris egyenletrendszert inverz segítségével:

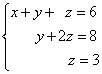
Megoldás. Ebben a trapézrendszerben a változó z egyedülálló módon megtalálható a harmadik egyenletből. Az értékét behelyettesítjük a második egyenletbe, és megkapjuk a változó értékét y:

Most már tudjuk két változó értékét - zÉs y. Behelyettesítjük őket az első egyenletbe, és megkapjuk a változó értékét x:

Az előző lépésekből kiírjuk az egyenletrendszer megoldását:

Egy ilyen trapéz alakú lineáris egyenletrendszer megszerzéséhez, amelyet nagyon egyszerűen megoldottunk, a lineáris egyenletrendszer elemi transzformációihoz kapcsolódó előre húzást kell használni. Szintén nem túl nehéz.

Lineáris egyenletrendszer elemi transzformációi

A rendszer egyenleteinek algebrai összeadásának iskolai módszerét megismételve azt találtuk, hogy a rendszer egyik egyenletéhez hozzáadhatjuk a rendszer egy másik egyenletét, és mindegyik egyenlet megszorozható néhány számmal. Ennek eredményeként ezzel egyenértékű lineáris egyenletrendszert kapunk. Ebben egy egyenlet már csak egy változót tartalmazott, amelynek értékét más egyenletekkel helyettesítve jutunk el a megoldáshoz. Az ilyen kiegészítés a rendszer elemi átalakításának egyik fajtája. A Gauss-módszer alkalmazásakor többféle transzformációt alkalmazhatunk.

A fenti animáció azt mutatja be, hogyan válik az egyenletrendszer fokozatosan trapéz alakúvá. Vagyis az, amelyet a legelső animációban látott, és meggyőzte magát, hogy könnyű megtalálni belőle minden ismeretlen értékét. Az ilyen átalakítások végrehajtásának módját és természetesen a példákat a továbbiakban tárgyaljuk.

Tetszőleges számú egyenletből és ismeretlenből álló lineáris egyenletrendszerek megoldása során az egyenletrendszerben és a rendszer kiterjesztett mátrixában Tud:

sorok átrendezése (erről a cikk elején volt szó);
ha más átalakítások egyenlő vagy arányos sorokat eredményeznek, egy kivételével törölhetők;
távolítsa el a „nulla” sorokat, ahol minden együttható nullával egyenlő;
tetszőleges karakterláncot szorozni vagy osztani egy bizonyos számmal;
bármely sorhoz adjon hozzá egy másik sort, megszorozva egy bizonyos számmal.

A transzformációk eredményeként ezzel egyenértékű lineáris egyenletrendszert kapunk.

Algoritmus és példák lineáris egyenletrendszer megoldására a rendszer négyzetmátrixával Gauss módszerrel

Tekintsük először olyan lineáris egyenletrendszerek megoldását, amelyekben az ismeretlenek száma egyenlő az egyenletek számával. Egy ilyen rendszer mátrixa négyzet, vagyis a benne lévő sorok száma megegyezik az oszlopok számával.

2. példa Oldjon meg egy lineáris egyenletrendszert Gauss módszerrel!

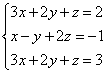
Lineáris egyenletrendszerek megoldása iskolai módokon, az egyenletek egyikét tagonként megszoroztuk egy bizonyos számmal, így a két egyenletben az első változó együtthatói ellentétes számok voltak. Egyenletek összeadásakor ez a változó megszűnik. A Gauss-módszer hasonlóan működik.

Egyszerűsíteni kinézet megoldásokat hozzuk létre a rendszer kiterjesztett mátrixát:

Ebben a mátrixban az ismeretlenek együtthatói a függőleges vonal előtt bal oldalon, a szabad tagok pedig a függőleges vonal után jobb oldalon helyezkednek el.

A változók osztási együtthatóinak megkönnyítése érdekében (az egységnyi osztás érdekében) Cseréljük fel a rendszermátrix első és második sorát. Ezzel egyenértékű rendszert kapunk, mivel egy lineáris egyenletrendszerben az egyenletek felcserélhetők:

Az új első egyenlet használata szüntesse meg a változót x a második és az összes azt követő egyenletből. Ehhez a mátrix második sorához hozzáadjuk az első sort, megszorozva (esetünkben -vel), a harmadik sorhoz - az első sorhoz - megszorozva (esetünkben -val).

Ez azért lehetséges, mert

Ha háromnál több egyenlet lenne a rendszerünkben, akkor az összes következő egyenlethez hozzá kellene adni az első sort, megszorozva a megfelelő együtthatók arányával, mínusz előjellel.

Ennek eredményeként egy új egyenletrendszerrel egyenértékű mátrixot kapunk, amelyben minden egyenlet a másodiktól kezdve nem tartalmaznak változót x :

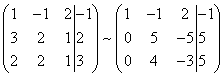
Az eredményül kapott rendszer második sorának egyszerűsítéséhez szorozzuk meg, és kapjuk meg egy ezzel a rendszerrel egyenértékű egyenletrendszer mátrixát:

Most az eredményül kapott rendszer első egyenletét változatlanul hagyva, a második egyenlet segítségével kiküszöböljük a változót y minden további egyenletből. Ehhez a rendszermátrix harmadik sorához hozzáadjuk a második sort, megszorozva ezzel (esetünkben -vel).

Ha háromnál több egyenlet lenne a rendszerünkben, akkor az összes következő egyenlethez egy második sort kellene hozzáadnunk, megszorozva a megfelelő mínusz előjellel vett együtthatók arányával.

Ennek eredményeként ismét egy olyan rendszer mátrixát kapjuk, amely ekvivalens ezzel a lineáris egyenletrendszerrel:

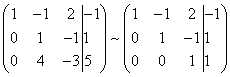
Egy ekvivalens trapéz alakú lineáris egyenletrendszert kaptunk:

Ha az egyenletek és változók száma nagyobb, mint a példánkban, akkor a változók szekvenciális eltávolításának folyamata addig folytatódik, amíg a rendszermátrix trapéz alakúvá nem válik, mint a demo példánkban.

Meg fogjuk találni a megoldást „a végétől” - a fordított lépés. Ezért az utolsó egyenletből határozzuk meg z:
.
Ezt az értéket behelyettesítve az előző egyenletbe, meg fogjuk találni y:

Az első egyenletből meg fogjuk találni x:

Válasz: ennek az egyenletrendszernek a megoldása az .

: ebben az esetben ugyanaz a válasz lesz, ha a rendszer egyedi megoldással rendelkezik. Ha a rendszernek végtelen számú megoldása van, akkor ez lesz a válasz, és ez a lecke ötödik részének témája.

Oldjon meg saját maga egy lineáris egyenletrendszert a Gauss-módszerrel, majd nézze meg a megoldást

Itt is van egy példa egy konzisztens és határozott lineáris egyenletrendszerre, amelyben az egyenletek száma egyenlő az ismeretlenek számával. A különbség a demópéldánktól az algoritmustól az, hogy már négy egyenlet és négy ismeretlen.

4. példa Oldjon meg egy lineáris egyenletrendszert Gauss módszerrel:

Most a második egyenletet kell használnia a változó eltávolításához a következő egyenletekből. Végezzük el az előkészítő munkát. Az együtthatók arányának kényelmesebbé tétele érdekében be kell szereznie egyet a második sor második oszlopában. Ehhez vonja ki a harmadikat a második sorból, és a kapott második sort szorozza meg -1-gyel.

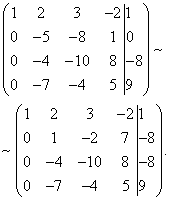
Végezzük el most a változó tényleges eltávolítását a harmadik és a negyedik egyenletből. Ehhez adja hozzá a második sort szorozva a harmadik sorhoz, a másodikat pedig a negyedikhez.

Most a harmadik egyenlet felhasználásával kivesszük a változót a negyedik egyenletből. Ehhez adja hozzá a harmadik sort a negyedikhez, megszorozva ezzel. Kiterjesztett trapézmátrixot kapunk.

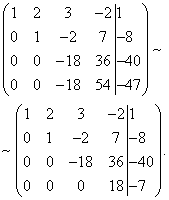
Kaptunk egy egyenletrendszert, amellyel az adott rendszer ekvivalens:

Ebből következően a kapott és adott rendszerek kompatibilisek és határozottak. Megtaláljuk a végső megoldást „a végétől”. A negyedik egyenletből közvetlenül kifejezhetjük az „x-négy” változó értékét:

Ezt az értéket behelyettesítjük a rendszer harmadik egyenletébe, és megkapjuk

Végül értékhelyettesítés

Az első egyenlet megadja

hol találjuk az „x first”-t:

Válasz: ennek az egyenletrendszernek van egyetlen döntés .

A rendszer megoldását Cramer módszerével kalkulátoron is ellenőrizhetjük: ebben az esetben ugyanazt a választ adjuk, ha a rendszer egyedi megoldással rendelkezik.

Alkalmazott feladatok megoldása Gauss-módszerrel ötvözetek feladatának példáján

Lineáris egyenletrendszereket használnak valós objektumok modellezésére a fizikai világban. Oldjuk meg az egyik ilyen problémát - az ötvözetek. Hasonló problémák a keverékekkel, az egyes áruk árucsoporton belüli költségével vagy részesedésével kapcsolatos problémák és hasonlók.

5. példa Három ötvözetdarab össztömege 150 kg. Az első ötvözet 60% rezet tartalmaz, a második - 30%, a harmadik - 10%. Ráadásul a második és a harmadik ötvözetben együttvéve 28,4 kg-mal kevesebb réz van, mint az első ötvözetben, a harmadik ötvözetben pedig 6,2 kg-mal kevesebb réz van, mint a másodikban. Keresse meg az ötvözet minden darabjának tömegét.

Megoldás. Összeállítunk egy lineáris egyenletrendszert:

A második és a harmadik egyenletet megszorozzuk 10-zel, így ekvivalens lineáris egyenletrendszert kapunk:

Elkészítjük a rendszer kiterjesztett mátrixát:

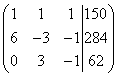
Figyelem, egyenesen előre. Egy sor összeadásával (esetünkben kivonva) egy sor szorzatát egy számmal (kétszer alkalmazzuk), a rendszer kiterjesztett mátrixával a következő transzformációk történnek:

A közvetlen lépésnek vége. Kiterjesztett trapézmátrixot kaptunk.

A fordított lépést alkalmazzuk. A megoldást a végétől megtaláljuk. Ezt látjuk.

A második egyenletből azt találjuk

A harmadik egyenletből -

A rendszer megoldását Cramer módszerével kalkulátoron is ellenőrizhetjük: ebben az esetben ugyanazt a választ adjuk, ha a rendszer egyedi megoldással rendelkezik.

Gauss módszerének egyszerűségét bizonyítja, hogy Carl Friedrich Gauss német matematikusnak mindössze 15 percébe telt kitalálni. A róla elnevezett módszer mellett Gauss műveiből ismert a „nem szabad összetéveszteni azt a mondást, ami számunkra hihetetlennek és természetellenesnek tűnik az abszolút lehetetlennel”. rövid utasításokat felfedezéseket tenni.

Sok alkalmazott feladatban előfordulhat, hogy nincs harmadik megszorítás, azaz harmadik egyenlet, akkor meg kell oldani egy két egyenletrendszert három ismeretlennel Gauss-módszerrel, vagy fordítva, kevesebb az ismeretlen, mint az egyenlet. Most elkezdjük az ilyen egyenletrendszerek megoldását.

A Gauss-módszer segítségével meghatározhatja, hogy bármely rendszer kompatibilis-e vagy nem n lineáris egyenletek -val n változók.

A Gauss-módszer és végtelen számú megoldású lineáris egyenletrendszerek

A következő példa egy konzisztens, de határozatlan lineáris egyenletrendszer, vagyis végtelen számú megoldással.

A rendszer kibővített mátrixában végrehajtott átalakítások (sorok átrendezése, sorok szorzása és osztása egy bizonyos számmal, újabb hozzáadása egy sorhoz) után megjelenhetnek az űrlap sorai.

Ha minden olyan egyenletben, amelynek alakja

A szabad tagok egyenlők nullával, ez azt jelenti, hogy a rendszer határozatlan, azaz végtelen számú megoldása van, és az ilyen típusú egyenletek „feleslegesek”, és kizárjuk őket a rendszerből.

6. példa.

Megoldás. Hozzuk létre a rendszer kiterjesztett mátrixát. Ezután az első egyenlet felhasználásával a változót kivesszük a következő egyenletekből. Ehhez adja hozzá a második, harmadik és negyedik sorhoz az elsőt, megszorozva a következővel:

Most adjuk hozzá a második sort a harmadikhoz és a negyedikhez.

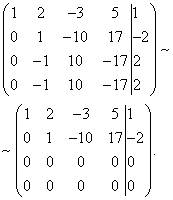
Ennek eredményeként eljutunk a rendszerhez

Az utolsó két egyenlet a forma egyenletévé változott. Ezek az egyenletek az ismeretlenek bármely értékére teljesülnek, és elvethetők.

A második egyenlet teljesítéséhez tetszőleges értéket választhatunk a és számára, ekkor a for érték egyedileg kerül meghatározásra: . Az első egyenletből az értéke is egyedileg megtalálható: .

Mind az adott, mind az utolsó rendszer konzisztens, de bizonytalan, és a képletek

tetszőlegesre, és adja meg nekünk egy adott rendszer összes megoldását.

Gauss-módszer és megoldás nélküli lineáris egyenletrendszerek

A következő példa egy inkonzisztens lineáris egyenletrendszer, vagyis olyan, amelynek nincs megoldása. Az ilyen problémákra a válasz így fogalmazódik meg: a rendszernek nincs megoldása.

Ahogy az első példa kapcsán már említettük, transzformációk végrehajtása után az űrlap sorai megjelenhetnek a rendszer kiterjesztett mátrixában

forma egyenletének felel meg

Ha van köztük legalább egy egyenlet nullától eltérő szabad taggal (azaz ), akkor ez az egyenletrendszer inkonzisztens, azaz nincs megoldása és megoldása teljes.

7. példa. Oldja meg a lineáris egyenletrendszert Gauss módszerrel:

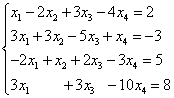
Megoldás. Összeállítjuk a rendszer kiterjesztett mátrixát. Az első egyenlet felhasználásával kizárjuk a változót a következő egyenletekből. Ehhez adja hozzá az első sort szorozva a második sorhoz, az első sort szorozva a harmadik sorhoz és az első sort a negyedik sorhoz.

Most a második egyenletet kell használnia a változó eltávolításához a következő egyenletekből. Az együtthatók egész arányának eléréséhez felcseréljük a rendszer kiterjesztett mátrixának második és harmadik sorát.

A harmadik és negyedik egyenlet kizárásához adja hozzá a másodikat szorozva a harmadik sorhoz, és a másodikat szorozva a negyedik sorhoz.

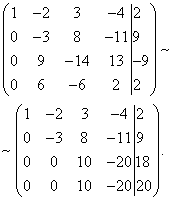
Most a harmadik egyenletet használva kivesszük a változót a negyedik egyenletből. Ehhez adja hozzá a harmadik sort a negyedik sorhoz, megszorozva ezzel.

Meghatározott rendszer tehát egyenértékű a következővel:

A kapott rendszer inkonzisztens, mivel utolsó egyenlete nem teljesíthető az ismeretlenek egyetlen értékével sem. Ezért ennek a rendszernek nincsenek megoldásai.

Ebben a cikkben a módszert lineáris egyenletrendszerek (SLAE) megoldási módszerének tekintjük. A módszer analitikus, azaz lehetővé teszi egy megoldási algoritmus beírását Általános nézet, majd helyettesítsd be az ott található konkrét példákból származó értékeket. A mátrixmódszerrel vagy a Cramer-képletekkel ellentétben lineáris egyenletrendszer Gauss-módszerrel történő megoldása során olyanokkal is dolgozhatunk, amelyeknek végtelen számú megoldása van. Vagy egyáltalán nincs meg nekik.

Mit jelent Gauss-módszerrel megoldani?

Először is fel kell írnunk az egyenletrendszerünket a Így néz ki. Vegyük a rendszert:

Az együtthatók táblázat formájában, a szabad kifejezések pedig külön oszlopban a jobb oldalon. A szabad kifejezéseket tartalmazó oszlop a kényelem kedvéért el van választva. Az ezt az oszlopot tartalmazó mátrixot kiterjesztettnek nevezzük.

Ezután az együtthatókkal rendelkező fő mátrixot egy felső háromszög alakúra kell redukálni. Ez a fő pontja a rendszer Gauss-módszerrel történő megoldásának. Egyszerűen fogalmazva, bizonyos manipulációk után a mátrixnak úgy kell kinéznie, hogy a bal alsó része csak nullákat tartalmazzon:

Ezután, ha az új mátrixot ismét egyenletrendszerként írod fel, észre fogod venni, hogy az utolsó sor már tartalmazza az egyik gyök értékét, amelyet aztán behelyettesítenek a fenti egyenletbe, egy másik gyökér található, és így tovább.

Ez a Gauss-módszer szerinti megoldás leírása a legáltalánosabb kifejezésekkel. Mi történik, ha hirtelen a rendszernek nincs megoldása? Vagy végtelenül sok van belőlük? Ezen és sok más kérdés megválaszolásához külön figyelembe kell venni a Gauss-módszer megoldásában használt összes elemet.

Mátrixok, tulajdonságaik

A mátrixban nincs rejtett jelentés. Ez egyszerűen egy kényelmes módja az adatok rögzítésének a vele végzett későbbi műveletekhez. Még az iskolásoknak sem kell félniük tőlük.

A mátrix mindig téglalap alakú, mert kényelmesebb. Még a Gauss-módszerben is, ahol minden egy háromszög alakú mátrix megalkotásán múlik, egy téglalap jelenik meg a bejegyzésben, csak nullákkal azon a helyen, ahol nincsenek számok. Lehet, hogy a nullákat nem írják le, de beleértettek.

A mátrixnak van mérete. A „szélessége” a sorok száma (m), a „hossza” az oszlopok száma (n). Ezután az A mátrix mérete (a jelölésükre általában nagybetűket használnak) leveleket) jelölése A m×n. Ha m=n, akkor ez a mátrix négyzet, és m=n a sorrendje. Ennek megfelelően az A mátrix bármely eleme jelölhető sor- és oszlopszámaival: a xy ; x - sorszám, változások, y - oszlopszám, változások.

B nem a döntés lényege. Elvileg minden művelet közvetlenül végrehajtható magával az egyenletekkel, de a jelölés sokkal körülményesebb lesz, és sokkal könnyebben összezavarodhatunk benne.

Döntő

A mátrixnak is van determinánsa. Ez egy nagyon fontos jellemző. Nem kell most kideríteni a jelentését, egyszerűen megmutathatja, hogyan számítják ki, majd megmondhatja, hogy a mátrix mely tulajdonságait határozza meg. A determináns megtalálásának legegyszerűbb módja az átlók segítségével. A mátrixban képzeletbeli átlókat rajzolnak; az mindegyiken elhelyezkedő elemeket megszorozzuk, majd a kapott szorzatokat összeadjuk: jobbra lejtős átlók - pluszjellel, balra lejtéssel - mínusz előjellel.

Rendkívül fontos megjegyezni, hogy a determináns csak négyzetmátrixra számítható. Téglalap alakú mátrix esetén a következőket teheti: válassza ki a legkisebbet a sorok és az oszlopok számából (legyen k), majd véletlenszerűen jelöljön ki a mátrixban k oszlopot és k sort. A kijelölt oszlopok és sorok metszéspontjában lévő elemek új négyzetmátrixot alkotnak. Ha egy ilyen mátrix determinánsa nem nulla szám, akkor az eredeti téglalap alakú mátrix alap-molljának nevezzük.

Mielőtt elkezdené egy egyenletrendszer Gauss-módszerrel történő megoldását, nem árt kiszámolni a determinánst. Ha kiderül, hogy nulla, akkor azonnal kijelenthetjük, hogy a mátrixnak vagy végtelen számú megoldása van, vagy nincs is. Ilyen szomorú esetben tovább kell menni, és megtudni a mátrix rangját.

Rendszerbesorolás

Van olyan, hogy egy mátrix rangja. Ez a nem nulla determináns maximális sorrendje (ha emlékszünk az alap-mollra, akkor azt mondhatjuk, hogy egy mátrix rangja az alap-moll sorrendje).

A ranggal kapcsolatos helyzet alapján az SLAE a következőkre osztható:

Közös. U A közös rendszerekben a fő mátrix rangja (amely csak együtthatókból áll) egybeesik a kiterjesztett mátrix rangjával (szabad tagok oszlopával). Az ilyen rendszereknek van megoldása, de nem feltétlenül egy, ezért a csuklós rendszereket további részekre osztják:
- bizonyos- egyetlen megoldással. Bizonyos rendszerekben a mátrix rangja és az ismeretlenek száma (vagy az oszlopok száma, ami ugyanaz) egyenlő;
- határozatlan - végtelen számú megoldással. Az ilyen rendszerekben a mátrixok rangja kisebb, mint az ismeretlenek száma.
Összeegyeztethetetlen. U Az ilyen rendszerekben a fő és a kiterjesztett mátrixok rangjai nem esnek egybe. Az inkompatibilis rendszereknek nincs megoldása.

A Gauss-módszer azért jó, mert a megoldás során vagy egyértelmû bizonyítást kapunk a rendszer inkonzisztenciájáról (anélkül, hogy nagy mátrixok determinánsait számolnánk), vagy egy végtelen számú megoldású rendszerre általános formájú megoldást kaphatunk.

Elemi átalakulások

Mielőtt közvetlenül a rendszer megoldásához kezdene, kevésbé nehézkessé és kényelmesebbé teheti a számításokat. Ezt elemi átalakításokkal érik el – úgy, hogy azok végrehajtása semmilyen módon nem változtatja meg a végső választ. Megjegyzendő, hogy a megadott elemi transzformációk egy része csak olyan mátrixokra érvényes, amelyek forrása az SLAE volt. Íme az átalakítások listája:

A húrok átrendezése. Nyilvánvaló, hogy ha megváltoztatja az egyenletek sorrendjét a rendszerrekordban, az semmilyen módon nem befolyásolja a megoldást. Következésképpen ennek a rendszernek a mátrixában a sorok is felcserélhetők, természetesen nem feledkezve meg a szabad kifejezések oszlopáról.
Egy karakterlánc összes elemének megszorzása egy bizonyos együtthatóval. Nagyon hasznos! Használható rövidítésre nagy számok a mátrixban, vagy távolítsa el a nullákat. Sok döntés, mint általában, nem változik, de a további műveletek kényelmesebbé válnak. A lényeg az, hogy az együttható ne legyen egyenlő nullával.
Sorok eltávolítása arányos tényezőkkel. Ez részben az előző bekezdésből következik. Ha egy mátrixban két vagy több sor arányos együtthatóval rendelkezik, akkor az egyik sort az arányossági együtthatóval szorozva/osztva két (vagy ismételten több) teljesen azonos sort kapunk, és a feleslegeseket eltávolíthatjuk, így marad. csak egy.
Null sor eltávolítása. Ha a transzformáció során valahol olyan sort kapunk, amelyben minden elem, beleértve a szabad tagot is, nulla, akkor az ilyen sort nullának nevezhetjük és kidobhatjuk a mátrixból.
Egy sor elemeihez hozzáadjuk a másik sor elemeit (a megfelelő oszlopokban), megszorozva egy bizonyos együtthatóval. A legnyilvánvalóbb és legfontosabb átalakulás. Érdemes részletesebben foglalkozni vele.

Tényezővel szorzott karakterlánc hozzáadása

A könnyebb érthetőség érdekében érdemes ezt a folyamatot lépésről lépésre lebontani. Két sort vettünk a mátrixból:

a 11 a 12 ... a 1n | b1

a 21 a 22 ... a 2n | b 2

Tegyük fel, hogy hozzá kell adni az elsőt a másodikhoz, meg kell szorozni a "-2" együtthatóval.

a" 21 = a 21 + -2 × a 11

a" 22 = a 22 + -2 × a 12

a" 2n = a 2n + -2×a 1n

Ezután a mátrix második sora egy újra cserélődik, és az első változatlan marad.

a 11 a 12 ... a 1n | b1

a" 21 a" 22 ... a" 2n | b 2

Megjegyzendő, hogy a szorzási együtthatót úgy is meg lehet választani, hogy két sor összeadása következtében az új sor egyik eleme nullával egyenlő. Ezért lehetséges egy egyenlet egy olyan rendszerben, ahol eggyel kevesebb ismeretlen lesz. És ha két ilyen egyenletet kapunk, akkor a műveletet meg lehet ismételni, és egy olyan egyenletet kapunk, amely kettővel kevesebb ismeretlent tartalmaz. És ha minden alkalommal nullára fordítja az összes, az eredeti alatti sor egy együtthatóját, akkor a lépcsőkhöz hasonlóan lemehet a mátrix legaljára, és kaphat egy egyenletet egy ismeretlennel. Ezt a rendszer Gauss-módszerrel történő megoldásának nevezzük.

Általában

Legyen rendszer. M egyenlete és n ismeretlen gyöke van. A következőképpen írhatod:

A fő mátrixot a rendszer együtthatóiból állítják össze. A kibővített mátrixhoz hozzáadunk egy szabad kifejezéseket tartalmazó oszlopot, és az egyszerűség kedvéért egy sor választja el őket.

a mátrix első sorát megszorozzuk a k = (-a 21 /a 11) együtthatóval;
a mátrix első módosított sora és második sora hozzáadásra kerül;
a második sor helyett az előző bekezdésből származó összeadás eredménye kerül be a mátrixba;
most az első együttható az új második sorban a 11 × (-a 21 /a 11) + a 21 = -a 21 + a 21 = 0.

Most ugyanazt az átalakítási sorozatot hajtják végre, csak az első és a harmadik sor érintett. Ennek megfelelően az algoritmus minden lépésében az a 21 elemet 31-re cseréljük. Ezután minden megismétlődik egy 41, ... egy m1-re. Az eredmény egy mátrix, ahol a sorok első eleme nulla. Most el kell felejtenie az első sort, és ugyanazt az algoritmust kell végrehajtania, a második sortól kezdve:

együttható k = (-a 32 /a 22);
a második módosított sor hozzáadódik az „aktuális” sorhoz;
az összeadás eredményét behelyettesítjük a harmadik, negyedik és így tovább sorba, miközben az első és a második változatlan marad;
a mátrix soraiban az első két elem már egyenlő nullával.

Az algoritmust addig kell ismételni, amíg a k = (-a m,m-1 /a mm) együttható meg nem jelenik. Ez azt jelenti, hogy az algoritmus legutóbbi végrehajtása csak az alsó egyenletre volt. Most a mátrix úgy néz ki, mint egy háromszög, vagy lépcsős alakú. Az alsó sorban ott van az a mn × x n = b m egyenlőség. Ismert az együttható és a szabad tag, ezeken keresztül fejeződik ki a gyök: x n = b m /a mn. Az eredményül kapott gyöket behelyettesítjük a felső sorba, hogy megtaláljuk x n-1 = (b m-1 - a m-1,n ×(b m /a mn))÷a m-1,n-1. És így tovább analógia útján: minden következő sorban van egy új gyökér, és miután elérte a rendszer „tetejét”, sok megoldást találhat. Ez lesz az egyetlen.

Amikor nincsenek megoldások

Ha az egyik mátrixsorban a szabad tag kivételével minden elem nulla, akkor az ennek a sornak megfelelő egyenlet 0 = b. Nincs megoldása. És mivel egy ilyen egyenlet benne van a rendszerben, akkor az egész rendszer megoldásainak halmaza üres, azaz degenerált.

Amikor végtelen számú megoldás létezik

Előfordulhat, hogy az adott háromszögmátrixban nincsenek olyan sorok, amelyekben az egyenlet egy együttható eleme és egy szabad tagja lenne. Csak olyan sorok vannak, amelyek átírva két vagy több változót tartalmazó egyenletnek tűnnek. Ez azt jelenti, hogy a rendszernek végtelen számú megoldása van. Ebben az esetben a válasz általános megoldás formájában adható meg. Hogyan kell csinálni?

A mátrix összes változója alap és szabad változókra van felosztva. Az alapvetőek azok, amelyek a lépésmátrixban a sorok „szélén” állnak. A többi ingyenes. Az általános megoldásban az alapváltozókat szabadon keresztül írjuk.

A kényelem kedvéért a mátrixot először visszaírják egy egyenletrendszerbe. Aztán az utolsóban, ahol pontosan csak egy alapváltozó maradt, az egyik oldalon marad, és minden más átkerül a másikra. Ez minden egyenletre egy alapváltozóval történik. Ezután a többi egyenletben, ahol lehetséges, az alapváltozó helyett a rá kapott kifejezést helyettesítjük. Ha az eredmény ismét csak egy alapváltozót tartalmazó kifejezés, akkor onnantól ismét kifejeződik, és így tovább, amíg minden alapváltozót szabad változókkal rendelkező kifejezésként fel nem írunk. Ez a SLAE általános megoldása.

Megtalálhatja a rendszer alapmegoldását is - adjon meg tetszőleges értéket a szabad változóknak, majd erre a konkrét esetre számítsa ki az alapváltozók értékeit. Végtelen számú konkrét megoldás adható.

Megoldás konkrét példákkal

Itt van egy egyenletrendszer.

A kényelem érdekében jobb, ha azonnal létrehozza a mátrixát

Ismeretes, hogy Gauss-módszerrel megoldva az első sornak megfelelő egyenlet változatlan marad a transzformációk végén. Ezért jövedelmezőbb lesz, ha a mátrix bal felső eleme a legkisebb - akkor a műveletek után a fennmaradó sorok első elemei nullára fordulnak. Ez azt jelenti, hogy az összeállított mátrixban előnyös lesz az első sor helyett a második sort tenni.

második sor: k = (-a 21 /a 11) = (-3/1) = -3

a" 21 = a 21 + k×a 11 = 3 + (-3) × 1 = 0

a" 22 = a 22 + k×a 12 = -1 + (-3) × 2 = -7

a" 23 = a 23 + k×a 13 = 1 + (-3) × 4 = -11

b" 2 = b 2 + k × b 1 = 12 + (-3) × 12 = -24

harmadik sor: k = (-a 3 1 /a 11) = (-5/1) = -5

a" 3 1 = a 3 1 + k × a 11 = 5 + (-5) × 1 = 0

a" 3 2 = a 3 2 + k × a 12 = 1 + (-5) × 2 = -9

a" 3 3 = a 33 + k × a 13 = 2 + (-5) × 4 = -18

b" 3 = b 3 + k × b 1 = 3 + (-5) × 12 = -57

Most, hogy ne keveredjen össze, fel kell írnia egy mátrixot a transzformációk közbenső eredményeivel.

Nyilvánvaló, hogy egy ilyen mátrix bizonyos műveletek segítségével kényelmesebbé tehető az észleléshez. Például eltávolíthatja az összes „mínuszt” a második sorból, ha minden elemet „-1”-gyel megszoroz.

Azt is érdemes megjegyezni, hogy a harmadik sorban minden elem három többszöröse. Ezután lerövidítheti a karakterláncot ezzel a számmal, minden elemet megszorozva "-1/3"-mal (mínusz - ugyanakkor a negatív értékek eltávolításához).

Sokkal szebben néz ki. Most békén kell hagynunk az első sort, és dolgozni a másodikkal és a harmadikkal. A feladat az, hogy a második sort hozzá kell adni a harmadikhoz, megszorozva olyan együtthatóval, hogy az a 32 elem nullával egyenlő legyen.

k = (-a 32 /a 22) = (-3/7) = -3/7 (ha néhány transzformáció során a válasz nem egész szám, akkor ajánlott a számítások pontosságának megőrzése a kilépéshez „ahogy van”, formában közönséges tört, és csak ezután, a válaszok beérkezése után döntse el, hogy kerekíti-e, és átváltja-e egy másik rögzítési formára)

a" 32 = a 32 + k × a 22 = 3 + (-3/7) × 7 = 3 + (-3) = 0

a" 33 = a 33 + k × a 23 = 6 + (-3/7) × 11 = -9/7

b" 3 = b 3 + k × b 2 = 19 + (-3/7) × 24 = -61/7

A mátrix újra új értékekkel íródik.

1	2	4	12
0	7	11	24
0	0	-9/7	-61/7

Amint látható, a kapott mátrixnak már van lépcsős formája. Ezért nincs szükség a rendszer további átalakításaira a Gauss-módszerrel. Itt mit lehet tenni, hogy eltávolítjuk a harmadik sorból általános együttható "-1/7".

Most minden gyönyörű. Nincs más hátra, mint a mátrix újraírása egyenletrendszer formájában, és a gyökök kiszámítása

x + 2y + 4z = 12 (1)

7y + 11z = 24 (2)

Azt az algoritmust, amellyel a gyököket most megtaláljuk, a Gauss-módszerben fordított mozgásnak nevezzük. A (3) egyenlet tartalmazza a z értéket:

y = (24 - 11×(61/9))/7 = -65/9

És az első egyenlet lehetővé teszi, hogy megtaláljuk x-et:

x = (12 - 4z - 2y)/1 = 12 - 4 × (61/9) - 2 × (-65/9) = -6/9 = -2/3

Jogunk van egy ilyen rendszert együttesnek, sőt határozottnak nevezni, vagyis egyedi megoldással. A választ a következő formában írjuk:

x 1 = -2/3, y = -65/9, z = 61/9.

Példa egy bizonytalan rendszerre

Egy adott rendszer Gauss-módszerrel történő megoldásának változatát elemeztük, most azt az esetet kell figyelembe venni, ha a rendszer bizonytalan, vagyis végtelenül sok megoldást találhatunk rá.

x 1 + x 2 + x 3 + x 4 + x 5 = 7 (1)

3x 1 + 2x 2 + x 3 + x 4 - 3x 5 = -2 (2)

x 2 + 2x 3 + 2x 4 + 6x 5 = 23 (3)

5x 1 + 4x 2 + 3x 3 + 3x 4 - x 5 = 12 (4)

Már a rendszer megjelenése is riasztó, mert az ismeretlenek száma n = 5, és a rendszermátrix rangja már pontosan kisebb ennél, mert a sorok száma m = 4, azaz a determinánsnégyzet legmagasabb rendje 4. Ez azt jelenti, hogy végtelen sok megoldás létezik, és meg kell keresni az általános megjelenését. A lineáris egyenletek Gauss-módszere lehetővé teszi ezt.

Először, mint általában, egy kiterjesztett mátrixot állítanak össze.

Második sor: együttható k = (-a 21 /a 11) = -3. A harmadik sorban az első elem az átalakítások előtt van, tehát nem kell hozzányúlni semmihez, hanem úgy kell hagyni, ahogy van. Negyedik sor: k = (-a 4 1 /a 11) = -5

Ha az első sor elemeit egymás után megszorozzuk az egyes együtthatóikkal, és hozzáadjuk a szükséges sorokhoz, a következő alakú mátrixot kapjuk:

Mint látható, a második, harmadik és negyedik sor egymással arányos elemekből áll. A második és a negyedik általában azonos, így az egyiket azonnal eltávolíthatjuk, a maradékot pedig megszorozhatjuk a „-1” együtthatóval, és megkapjuk a 3-as sort. És ismét két azonos sorból hagyjunk egyet.

Az eredmény egy ilyen mátrix. Bár a rendszert még nem írták le, itt meg kell határozni az alapvető változókat - az a 11 = 1 és a 22 = 1 együtthatónál állókat, illetve a szabadokat - a többit.

A második egyenletben csak egy alapváltozó van - x 2. Ez azt jelenti, hogy onnantól az x 3 , x 4 , x 5 változókon keresztül írva kifejezhető, amelyek szabadok.

A kapott kifejezést behelyettesítjük az első egyenletbe.

Az eredmény egy egyenlet, amelyben az egyetlen alapváltozó x 1. Tegyük meg vele ugyanazt, mint az x 2-vel.

Az összes alapvető változót, amelyből kettő van, három szabad változóval fejezzük ki.

Megadhatja a rendszer egyik konkrét megoldását is. Ilyen esetekben általában nullákat választanak a szabad változók értékeként. Akkor ez lesz a válasz:

16, 23, 0, 0, 0.

Példa a nem együttműködő rendszerre

Megoldás nem kompatibilis rendszerek egyenletek a Gauss-módszerrel - a leggyorsabb. Azonnal véget ér, amint az egyik szakaszban olyan egyenletet kapunk, amelynek nincs megoldása. Vagyis a gyökerek kiszámításának szakasza, amely meglehetősen hosszú és fárasztó, megszűnik. A következő rendszert veszik figyelembe:

x + y - z = 0 (1)

2x - y - z = -2 (2)

4x + y - 3z = 5 (3)

Szokás szerint a mátrix összeállítása:

1	1	-1	0
2	-1	-1	-2
4	1	-3	5

És lépésenkénti formára redukálódik:

k 1 = -2k 2 = -4

1	1	-1	0
0	-3	1	-2
0	0	0	7

Az első transzformáció után a harmadik sor a forma egyenletét tartalmazza

megoldás nélkül. Következésképpen a rendszer inkonzisztens, és a válasz az üres halmaz lesz.

A módszer előnyei és hátrányai

Ha kiválasztja, hogy melyik módszert oldja meg az SLAE-k papíron egy tollal, akkor az ebben a cikkben tárgyalt módszer tűnik a legvonzóbbnak. Sokkal nehezebb összezavarodni az elemi transzformációkban, mintha kézzel kellene keresni egy determinánst vagy valami trükkös inverz mátrixot. Ha azonban programokat használ az ilyen típusú adatok kezelésére, pl. táblázatokat, akkor kiderül, hogy az ilyen programok már tartalmaznak algoritmusokat a mátrixok fő paramétereinek kiszámítására - determináns, minor, inverz stb. És ha biztos abban, hogy a gép ezeket az értékeket kiszámolja, és nem hibázik, akkor célszerűbb mátrix módszer vagy Cramer-képleteket, mert alkalmazásuk a determinánsok számításával kezdődik és végződik, ill inverz mátrixok.

Alkalmazás

Mivel a Gauss-féle megoldás egy algoritmus, a mátrix pedig valójában egy kétdimenziós tömb, programozásban használható. De mivel a cikk „a bábuknak” szóló útmutatónak tekinti magát, el kell mondanunk, hogy a módszert legegyszerűbben táblázatokba, például Excelbe lehet helyezni. Az Excel ismét kétdimenziós tömbnek tekinti a táblázatba mátrix formájában beírt SLAE-ket. A velük végzett műveletekhez pedig sok szép parancs létezik: összeadás (csak azonos méretű mátrixokat adhat hozzá!), szorzás számmal, mátrixok szorzása (bizonyos megkötésekkel is), az inverz és transzponált mátrixok megtalálása és ami a legfontosabb , a determináns kiszámítása. Ha ezt az időigényes feladatot egyetlen paranccsal helyettesítjük, sokkal gyorsabban meg lehet határozni a mátrix rangját, és így megállapítható a kompatibilitása vagy inkompatibilitása.

A 16-18. század eleje óta a matematikusok intenzíven elkezdték tanulmányozni a függvényeket, aminek köszönhetően életünkben annyi minden megváltozott. A számítástechnika egyszerűen nem létezne e tudás nélkül. Megoldásokért összetett feladatok, lineáris egyenletek és függvények, különféle fogalmak, tételek és megoldási technikák születtek. A lineáris egyenletek és rendszereik megoldásának egyik ilyen univerzális és racionális módszere és technikája a Gauss-módszer volt. Mátrixok, rangjuk, determináns - mindent ki lehet számítani bonyolult műveletek használata nélkül.

Mi az a SLAU

A matematikában létezik az SLAE fogalma - egy lineáris rendszer algebrai egyenletek. Írd őt körül? Ez egy m egyenlet halmaza a szükséges n ismeretlen mennyiséggel, amelyeket általában x, y, z vagy x 1, x 2 ... x n vagy más szimbólumokként jelölnek. Megoldás Gauss-módszerrel ezt a rendszert- azt jelenti, hogy megtalálja az összes ismeretlen ismeretlent. Ha egy rendszerben ugyanannyi ismeretlen és egyenlet van, akkor azt n-edrendű rendszernek nevezzük.

A legnépszerűbb módszerek az SLAE megoldására

BAN BEN oktatási intézmények A középiskolai hallgatók különféle módszereket tanulnak az ilyen rendszerek megoldására. Leggyakrabban ezek egyszerű egyenletek, amelyek két ismeretlenből állnak, tehát bármelyik létező módszer Nem sok időbe telik, hogy megtaláljuk a választ. Ez olyan lehet, mint egy helyettesítési módszer, amikor az egyik egyenletből egy másikat származtatunk, és behelyettesítünk az eredetibe. Vagy a tagonkénti kivonás és összeadás módszere. De a Gauss-módszert a legegyszerűbbnek és leguniverzálisabbnak tekintik. Lehetővé teszi tetszőleges számú ismeretlennel rendelkező egyenletek megoldását. Miért tekinthető racionálisnak ez a konkrét technika? Ez egyszerű. A mátrix módszerben az a jó, hogy nem kell többször átírni a szükségtelen szimbólumokat, elég az együtthatókon aritmetikai műveleteket végrehajtani – és megbízható eredményt kapunk.

Hol használják az SLAE-ket a gyakorlatban?

Az SLAE megoldása a függvények grafikonjain lévő egyenesek metszéspontjai. Csúcstechnológiás számítógépes korunkban azoknak az embereknek, akik szorosan kötődnek a játékok és egyéb programok fejlesztéséhez, tudniuk kell, hogyan oldják meg az ilyen rendszereket, mit képviselnek, és hogyan ellenőrizzék a kapott eredmény helyességét. Leggyakrabban a programozók speciális lineáris algebra kalkulátor programokat fejlesztenek, amelyek egy lineáris egyenletrendszert is tartalmaznak. A Gauss-módszer lehetővé teszi az összes létező megoldás kiszámítását. Más egyszerűsített képleteket és technikákat is alkalmaznak.

SLAU kompatibilitási kritérium

Egy ilyen rendszer csak akkor oldható meg, ha kompatibilis. Az érthetőség kedvéért ábrázoljuk az SLAE-t Ax=b formában. Van megoldása, ha rang(A) egyenlő rang(A,b). Ebben az esetben (A,b) egy kiterjesztett alakmátrix, amelyet az A mátrixból szabad tagokkal átírva kaphatunk. Kiderült, hogy a lineáris egyenletek megoldása a Gauss-módszerrel meglehetősen egyszerű.

Talán néhány szimbólum nem teljesen világos, ezért mindent egy példával kell megvizsgálni. Tegyük fel, hogy van egy rendszer: x+y=1; 2x-3y=6. Csak két egyenletből áll, amelyekben 2 ismeretlen van. A rendszernek csak akkor lesz megoldása, ha mátrixának rangja megegyezik a kiterjesztett mátrix rangjával. Mi az a rang? Ez a rendszer független vonalainak száma. Esetünkben a mátrix rangja 2. Az A mátrix az ismeretlenek közelében elhelyezkedő együtthatókból áll, és a „=” jel mögött elhelyezkedő együtthatók is beleférnek a kiterjesztett mátrixba.

Miért ábrázolhatók az SLAE-k mátrix formában?

A bizonyított Kronecker-Capelli-tétel szerinti kompatibilitási kritérium alapján egy lineáris algebrai egyenletrendszer ábrázolható mátrix formában. A Gauss-kaszkád módszerrel megoldhatja a mátrixot, és egyetlen megbízható választ kaphat az egész rendszerre. Ha egy közönséges mátrix rangja egyenlő a kiterjesztett mátrix rangjával, de kisebb, mint az ismeretlenek száma, akkor a rendszernek végtelen számú válasza van.

Mátrix transzformációk

Mielőtt rátérne a mátrixok megoldására, tudnia kell, milyen műveleteket lehet végrehajtani az elemeiken. Számos elemi átalakítás létezik:

A rendszer mátrix formájú átírásával és megoldásával a sorozat összes elemét meg lehet szorozni ugyanazzal az együtthatóval.
A mátrix kanonikus formájúvá alakításához két párhuzamos sort felcserélhet. A kanonikus forma azt jelenti, hogy minden mátrixelem, amely a főátló mentén helyezkedik el, egyes lesz, a fennmaradó elemek pedig nullák.
A mátrix párhuzamos sorainak megfelelő elemei egymáshoz adhatók.

Jordan-Gauss módszer

A lineáris homogén és inhomogén egyenletrendszerek Gauss-módszerrel történő megoldásának lényege az ismeretlenek fokozatos kiküszöbölése. Tegyük fel, hogy van egy két egyenletrendszerünk, amelyben két ismeretlen van. Ezek megtalálásához ellenőriznie kell a rendszer kompatibilitását. Az egyenletet a Gauss-módszer nagyon egyszerűen megoldja. Fel kell írni az egyes ismeretlenek közelében elhelyezkedő együtthatókat mátrix formában. A rendszer megoldásához ki kell írni a kiterjesztett mátrixot. Ha valamelyik egyenlet kevesebb ismeretlent tartalmaz, akkor a hiányzó elem helyére „0”-t kell tenni. A mátrixra minden ismert transzformációs módszert alkalmazunk: szorzást, osztást egy számmal, a sorozat megfelelő elemeinek összeadását és egyebeket. Kiderül, hogy minden sorban meg kell hagyni egy „1” értékű változót, a többit nullára kell csökkenteni. A pontosabb megértés érdekében érdemes a Gauss-módszert példákkal átgondolni.

Egy egyszerű példa a 2x2 rendszer megoldására

Kezdésként vegyünk egy egyszerű algebrai egyenletrendszert, amelyben 2 ismeretlen lesz.

Írjuk át egy kiterjesztett mátrixba.

Ennek a lineáris egyenletrendszernek a megoldásához mindössze két műveletre van szükség. A mátrixot kanonikus formára kell hoznunk, hogy a főátló mentén legyenek olyanok. Így a mátrixformából visszalépve a rendszerbe a következő egyenleteket kapjuk: 1x+0y=b1 és 0x+1y=b2, ahol b1 és b2 a kapott válasz a megoldási folyamatban.

A kiterjesztett mátrix megoldásának első lépése a következő lesz: az első sort meg kell szorozni -7-tel, és hozzá kell adni a megfelelő elemeket a második sorhoz, hogy megszabaduljunk egy ismeretlentől a második egyenletben.
Mivel az egyenletek Gauss-módszerrel történő megoldása magában foglalja a mátrix kanonikus formára való redukálását, ezért ugyanazokat a műveleteket kell végrehajtani az első egyenlettel, és el kell távolítani a második változót. Ehhez kivonjuk a második sort az elsőből, és megkapjuk a szükséges választ - az SLAE megoldását. Vagy az ábrán látható módon a második sort megszorozzuk -1-gyel, és a második sor elemeit hozzáadjuk az első sorhoz. Ez ugyanaz.

Mint látjuk, rendszerünket a Jordan-Gauss módszerrel oldottuk meg. Átírjuk a kívánt formában: x=-5, y=7.

Példa egy 3x3-as SLAE megoldásra

Tegyük fel, hogy van egy bonyolultabb lineáris egyenletrendszerünk. A Gauss-módszer lehetővé teszi a válasz kiszámítását még a legzavarosabbnak tűnő rendszerre is. Ezért annak érdekében, hogy mélyebben elmélyüljön a számítási módszertanban, továbbléphet többre összetett példa három ismeretlennel.

Az előző példához hasonlóan átírjuk a rendszert egy kiterjesztett mátrix formájában, és elkezdjük a kanonikus formába hozni.

A rendszer megoldásához sokkal több műveletet kell végrehajtania, mint az előző példában.

Először az első oszlopot egységnyi eleművé kell tenni, a többit pedig nullák. Ehhez szorozza meg az első egyenletet -1-gyel, és adja hozzá a második egyenletet. Fontos megjegyezni, hogy az első sort az eredeti, a második sort pedig módosított formában írjuk át.
Ezután eltávolítjuk ugyanezt az első ismeretlent a harmadik egyenletből. Ehhez szorozza meg az első sor elemeit -2-vel, és adja hozzá a harmadik sorhoz. Most az első és a második sor át van írva eredeti formájában, a harmadik pedig - változtatásokkal. Amint az eredményből látható, a mátrix főátlójának elején kaptuk az elsőt és a maradék nullákat. Még néhány lépés, és a Gauss-módszerrel készült egyenletrendszer megbízhatóan megoldódik.
Most műveleteket kell végrehajtania a sorok többi elemén. A harmadik és a negyedik művelet egybe kombinálható. A második és harmadik sort el kell osztanunk -1-gyel, hogy megszabaduljunk az átlón lévő mínuszoktól. A harmadik sort már a szükséges formára hoztuk.
Ezután a második sort kanonikus formára hozzuk. Ehhez a harmadik sor elemeit megszorozzuk -3-mal, és hozzáadjuk a mátrix második sorához. Az eredményből jól látható, hogy a második sor is a szükséges formára redukálódik. Még néhány műveletet kell végrehajtani, és eltávolítani az ismeretlenek együtthatóit az első sorból.
Ahhoz, hogy egy sor második eleméből 0 legyen, meg kell szorozni a harmadik sort -3-mal, és hozzá kell adni az első sorhoz.
A következő döntő lépés a második sor szükséges elemeinek hozzáadása az első sorhoz. Így megkapjuk a mátrix kanonikus formáját, és ennek megfelelően a választ.

Mint látható, az egyenletek Gauss-módszerrel történő megoldása meglehetősen egyszerű.

Példa egy 4x4-es egyenletrendszer megoldására

Néhány bonyolultabb egyenletrendszer a Gauss-módszerrel is megoldható számítógépes programok segítségével. Az ismeretlenek együtthatóit be kell írni a meglévő üres cellákba, és maga a program lépésről lépésre kiszámítja a kívánt eredményt, részletesen leírva az egyes műveleteket.

Az alábbiakban leírt lépésről lépésre szóló utasítás megoldásokat erre a példára.

Első lépésben az üres cellákba beírjuk az ismeretlenekhez tartozó szabad együtthatókat és számokat. Így ugyanazt a kiterjesztett mátrixot kapjuk, amelyet kézzel írunk.

És minden szükséges aritmetikai művelet végrehajtásra kerül, hogy a kiterjesztett mátrixot a kanonikus formába hozzuk. Meg kell érteni, hogy egy egyenletrendszerre nem mindig egész számok adhatók. Néha a megoldás törtszámokból adódik.

A megoldás helyességének ellenőrzése

A Jordan-Gauss módszer biztosítja az eredmény helyességének ellenőrzését. Annak érdekében, hogy megtudja, az együtthatók helyesen vannak-e kiszámítva, csak be kell cserélnie az eredményt az eredeti egyenletrendszerbe. Bal oldal az egyenleteknek egyezniük kell jobb oldal, amely az egyenlőségjel mögött található. Ha a válaszok nem egyeznek, akkor újra kell számolnia a rendszert, vagy meg kell próbálnia más, Ön által ismert SLAE-megoldási módszert alkalmazni, mint például a helyettesítés vagy a tagonkénti kivonás és összeadás. Végtére is, a matematika olyan tudomány, amelynek hatalmas száma van különféle technikák megoldásokat. De ne feledje: az eredménynek mindig ugyanannak kell lennie, függetlenül attól, hogy milyen megoldási módot használt.

Gauss módszer: a leggyakoribb hibák az SLAE megoldása során

Lineáris egyenletrendszerek megoldása során leggyakrabban olyan hibák fordulnak elő, mint például az együtthatók helytelen átvitele mátrix formába. Vannak olyan rendszerek, amelyekben néhány ismeretlen hiányzik az egyik egyenletből, majd egy kiterjesztett mátrixba történő adatátvitelkor elveszhetnek. Ennek eredményeként ennek a rendszernek a megoldása során előfordulhat, hogy az eredmény nem felel meg a ténylegesnek.

Egy másik nagy hiba lehet a végeredmény helytelen kiírása. Világosan meg kell érteni, hogy az első együttható megfelel az első ismeretlennek a rendszerből, a második - a másodiknak, és így tovább.

A Gauss-módszer részletesen leírja a lineáris egyenletek megoldását. Ennek köszönhetően könnyen előállítható szükséges műveleteketés megtalálja a helyes eredményt. Ezenkívül ez egy univerzális eszköz bármilyen bonyolultságú egyenletre megbízható válasz megtalálásához. Talán ezért használják olyan gyakran SLAE-k megoldása során.

Itt ingyenesen megoldhat egy lineáris egyenletrendszert Gauss módszer online nagy méretek komplex számokban igen részletes megoldással. Számológépünk a szokásos határozott és határozatlan lineáris egyenletrendszereket is meg tudja oldani online a Gauss-módszerrel, amelynek végtelen számú megoldása van. Ebben az esetben a válaszban néhány változó függőségét más, szabadon keresztül kapja meg. A Gauss-megoldás segítségével online is ellenőrizheti az egyenletrendszer konzisztenciáját.

A módszerről

Lineáris egyenletrendszer megoldása során online módszer Gauss a következő lépéseket hajtja végre.

Felírjuk a kiterjesztett mátrixot.
Valójában a megoldás a Gauss-módszer előre és hátra lépéseire oszlik. A Gauss-módszer közvetlen megközelítése a mátrix redukciója lépcsőzetes formára. A Gauss-módszer fordítottja a mátrix redukálása speciális lépcsőzetes formára. De a gyakorlatban kényelmesebb azonnal nullázni azt, ami a kérdéses elem felett és alatt is található. Számológépünk pontosan ezt a módszert használja.
Fontos megjegyezni, hogy a Gauss-módszerrel történő megoldásnál a mátrixban legalább egy nulla sor jelenléte NEM nullával jobb oldal(szabad tagok oszlopa) a rendszer inkompatibilitását jelzi. Ebben az esetben a lineáris rendszerre nem létezik megoldás.

A Gauss-algoritmus online működésének legjobb megértéséhez írjon be egy példát, válassza ki a "nagyon részletes megoldás", és keresse meg a megoldását az interneten.

1. Lineáris algebrai egyenletrendszer

1.1 Lineáris algebrai egyenletrendszer fogalma

Az egyenletrendszer olyan feltétel, amely több egyenlet egyidejű végrehajtásából áll több változóra vonatkozóan. Az m egyenletet és n ismeretlent tartalmazó lineáris algebrai egyenletrendszert (a továbbiakban: SLAE) a következő formájú rendszernek nevezzük:

ahol az a ij számokat rendszeregyütthatóknak, a b i számokat szabad tagoknak nevezzük, a ijÉs b i(i=1,…, m; b=1,…, n) néhány ismert számot és x-et jelent 1 ,…, x n– ismeretlen. Az együtthatók kijelölésében a ij az első i index az egyenlet számát jelöli, a második j pedig annak az ismeretlennek a száma, amelynél ez az együttható áll. Meg kell találni az x n számokat. Kényelmes egy ilyen rendszert kompakt mátrix formában írni: AX=B. Itt A a rendszeregyütthatók mátrixa, amelyet főmátrixnak nevezünk;

– ismeretlenek oszlopvektora xj.
a bi szabad kifejezések oszlopvektora.

Az A*X mátrixok szorzata definiált, mivel az A mátrixban annyi oszlop van, ahány sor az X mátrixban (n darab).

Egy rendszer kiterjesztett mátrixa a rendszer A mátrixa, kiegészítve egy szabad tagok oszlopával

1.2 Lineáris algebrai egyenletrendszer megoldása

Az egyenletrendszer megoldása a számok (változók értéke) rendezett halmaza, amikor változók helyett helyettesítjük őket, a rendszer minden egyenlete valódi egyenlőséggé alakul.

Egy rendszer megoldása az x1=c1, x2=c2,…, xn=cn ismeretlenek n értéke, amelyek behelyettesítésével a rendszer összes egyenlete valódi egyenlőséggé válik. A rendszer bármely megoldása felírható oszlopmátrixként

Egy egyenletrendszert konzisztensnek nevezünk, ha legalább egy megoldása van, és inkonzisztensnek, ha nincs megoldása.

Egy konzisztens rendszert határozottnak nevezünk, ha egyetlen megoldása van, és határozatlannak, ha egynél több megoldása van. Ez utóbbi esetben mindegyik megoldását a rendszer egy adott megoldásának nevezzük. Az összes konkrét megoldás halmazát általános megoldásnak nevezzük.

Egy rendszer megoldása azt jelenti, hogy meg kell találni, hogy kompatibilis-e vagy inkonzisztens. Ha a rendszer konzisztens, keresse meg az általános megoldást.

Két rendszert ekvivalensnek (ekvivalensnek) nevezünk, ha ugyanaz az általános megoldás. Más szóval, a rendszerek ekvivalensek, ha az egyik megoldása a másik megoldása, és fordítva.

Átalakítás, melynek alkalmazása a rendszert a új rendszer, amely egyenértékű az eredetivel, egyenértékű vagy egyenértékű transzformációnak nevezzük. Példák az ekvivalens transzformációkra a következő transzformációk: egy rendszer két egyenletének felcserélése, két ismeretlen felcserélése az összes egyenlet együtthatóival együtt, egy rendszer bármely egyenletének mindkét oldalát megszorozzuk egy nem nulla számmal.

Egy lineáris egyenletrendszert homogénnek nevezünk, ha minden szabad tag nulla:

Egy homogén rendszer mindig konzisztens, mivel x1=x2=x3=…=xn=0 a rendszer megoldása. Ezt a megoldást nullának vagy triviálisnak nevezzük.

2. Gauss eliminációs módszer

2.1 A Gauss-eliminációs módszer lényege

A lineáris algebrai egyenletrendszerek megoldásának klasszikus módszere az ismeretlenek szekvenciális kiküszöbölésének módszere. Gauss módszer(Gauss eliminációs módszernek is nevezik). Ez egy módszer a változók szekvenciális eliminálására, amikor elemi transzformációk segítségével egy egyenletrendszert egy lépcsős (vagy háromszög alakú) ekvivalens rendszerré redukálunk, amelyből az összes többi változót szekvenciálisan megtaláljuk, az utolsótól kezdve. szám) változók.

A Gauss-módszert alkalmazó megoldási folyamat két szakaszból áll: előre és hátra mozgásból.

1. Közvetlen löket.

Az első szakaszban az úgynevezett direkt mozgatást hajtják végre, amikor a sorok feletti elemi átalakításokkal a rendszert lépcsőzetes vagy háromszög alakúra hozzuk, vagy megállapítják, hogy a rendszer nem kompatibilis. Ugyanis a mátrix első oszlopának elemei közül válasszunk ki egy nullától eltérő egyet, mozgassuk a legfelső pozícióba a sorok átrendezésével, és az így kapott első sort az átrendezés után vonjuk ki a fennmaradó sorokból, szorozzuk meg egy értékkel. egyenlő az egyes sorok első elemének az első sor első eleméhez viszonyított arányával, nullázva ezzel az alatta lévő oszlopot.

Miután ezek az átalakítások befejeződtek, az első sort és az első oszlopot gondolatban áthúzzuk, és addig folytatjuk, amíg egy nulla méretű mátrix nem marad. Ha bármelyik iterációnál nincs nullától eltérő elem az első oszlop elemei között, akkor lépjen a következő oszlopra, és hajtson végre hasonló műveletet.

Az első szakaszban (közvetlen löket) a rendszer lépcsőzetes (különösen háromszög alakú) formára redukálódik.

Az alábbi rendszer lépcsőzetes formája van:

Az aii együtthatókat a rendszer fő (vezető) elemeinek nevezzük.

(ha a11=0, rendezze át a mátrix sorait úgy, hogy a 11 nem egyenlő 0-val. Ez mindig lehetséges, mert különben a mátrix nulla oszlopot tartalmaz, determinánsa nulla, és a rendszer inkonzisztens).

Alakítsuk át a rendszert úgy, hogy az első kivételével minden egyenletből kiküszöböljük az ismeretlen x1-et (a rendszer elemi transzformációit használva). Ehhez meg kell szorozni az első egyenlet mindkét oldalát

és adjuk hozzá tagonként a rendszer második egyenletét (vagy a második egyenletből vonjuk ki tagonként az elsőt, szorozzuk meg -val). Ezután az első egyenlet mindkét oldalát megszorozzuk és hozzáadjuk a rendszer harmadik egyenletéhez (vagy a harmadikból kivonjuk az első egyenletet szorozva). Így az első sort egymás után megszorozzuk egy számmal, és hozzáadjuk én sor, for i= 2, 3, …,n.

Ezt a folyamatot folytatva egy egyenértékű rendszert kapunk:

– az ismeretlenek és a szabad tagok együtthatóinak új értékei a rendszer utolsó m-1 egyenleteiben, amelyeket a képletek határoznak meg:

Így az első lépésben minden, az a 11 első vezető elem alatti együttható megsemmisül

0, a második lépésben megsemmisülnek a második vezetőelem alatt fekvő elemek a 22 (1) (ha a 22 (1) 0) stb. Ezt a folyamatot tovább folytatva végül az (m-1) lépésnél az eredeti rendszert háromszögrendszerré redukáljuk.

Ha a rendszer lépcsőzetes formára redukálása során nulla egyenletek jelennek meg, pl. a 0=0 alakú egyenlőségeket el kell vetni. Ha megjelenik a forma egyenlete

akkor ez a rendszer inkompatibilitását jelzi.

Itt ér véget Gauss módszerének közvetlen fejlődése.

2. Fordított löket.

A második szakaszban az úgynevezett fordított mozgást hajtják végre, amelynek lényege, hogy az összes eredő alapváltozót nem alapváltozókkal fejezzük ki és konstruáljuk alapvető rendszer megoldásokat, vagy ha minden változó bázisos, akkor numerikusan fejezze ki a lineáris egyenletrendszer egyedi megoldását.

Ez az eljárás az utolsó egyenlettel kezdődik, amelyből a megfelelő alapváltozót kifejezzük (csak egy van benne), és behelyettesítjük az előző egyenletekbe, és így tovább, felfelé haladva a „lépéseket”.

Minden sor pontosan egy bázisváltozónak felel meg, így az utolsó (legfelső) kivételével minden lépésben a helyzet pontosan megismétli az utolsó sor esetét.

Megjegyzés: a gyakorlatban kényelmesebb nem a rendszerrel dolgozni, hanem annak kiterjesztett mátrixával, az összes elemi transzformációt a sorain végrehajtva. Célszerű, ha az a11 együttható 1-gyel egyenlő (rendezzük át az egyenleteket, vagy osszuk el az egyenlet mindkét oldalát a11-gyel).

2.2 Példák SLAE-k megoldására Gauss-módszerrel

Ebben a részben három különböző példán keresztül bemutatjuk, hogyan oldja meg a Gauss-módszer az SLAE-ket.

Példa 1. Oldjon meg egy 3. rendű SLAE-t.

Állítsuk vissza az együtthatókat a

a második és a harmadik sorban. Ehhez szorozza meg őket 2/3-mal és 1-gyel, és adja hozzá az első sorhoz: